
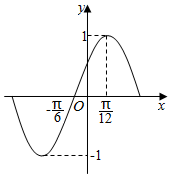
 如图是某函数图象的一部分,则该函数表达式是( )
如图是某函数图象的一部分,则该函数表达式是( )| A. | $y=cos(\frac{π}{6}-2x)$ | B. | $y=cos(2x-\frac{π}{3})$ | C. | $y=sin(x+\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
分析 根据三角函数的图象和性质,利用代入法和排除法进行判断即可.
解答 解:设函数的表达式为f(x)=Asin(ωx+φ)或f(x)=Acos(ωx+φ),
函数的最大值为1,都满足条件.
函数的周期T=4×[$\frac{π}{12}-(-\frac{π}{6})$]=4×$\frac{3π}{12}$=π,则ω=2,排除C.
当x=$\frac{π}{12}$时,函数取得最大值1,则$y=cos(\frac{π}{6}-2x)$=cos($\frac{π}{6}$-$\frac{π}{6}$)=cos0=1,满足条件.
$y=cos(2x-\frac{π}{3})$=cos($\frac{π}{6}$-$\frac{π}{3}$)=cos(-$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$≠1,排除B,
$y=sin(2x-\frac{π}{6})$=sin($\frac{π}{6}$-$\frac{π}{6}$)=sin0=0≠1,排除D,
故选:A.
点评 本题主要考查函数解析式的确定,根据函数的图象和性质,利用排除法以及验证法分别进行验证即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②④⑤ | C. | ④⑤ | D. | ②⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向右平移$\frac{5π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{5π}{6}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
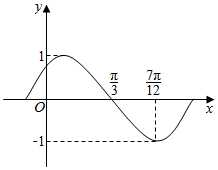 将函数$y=sin(ωx+φ)(ω>0,|φ|≤\frac{π}{2})$的图象沿x轴方向向左平移$\frac{π}{3}$个单位,所得曲线的一部分图象如图,则ω,φ的值分别为( )
将函数$y=sin(ωx+φ)(ω>0,|φ|≤\frac{π}{2})$的图象沿x轴方向向左平移$\frac{π}{3}$个单位,所得曲线的一部分图象如图,则ω,φ的值分别为( )| A. | 1,$\frac{π}{3}$ | B. | 1,$-\frac{π}{3}$ | C. | 2,$\frac{π}{3}$ | D. | 2,$-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-\frac{{4{y^2}}}{3}=1$ | B. | $\frac{{4{x^2}}}{3}-\frac{y^2}{3}=1$ | ||
| C. | $\frac{{4{x^2}}}{3}-\frac{y^2}{3}=1$或$\frac{x^2}{3}-\frac{{4{y^2}}}{3}=1$ | D. | $\frac{{4{y^2}}}{3}-\frac{x^2}{3}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com