
| A. | ①②③ | B. | ②④⑤ | C. | ④⑤ | D. | ②⑤ |
分析 ①α⊥β不一定成立,可能相交不垂直;
②利用面面垂直的判定定理可知α⊥β;
③由已知a⊥b,不一定成立;
④若a不垂直平面α,则a可能垂直于平面α内的无数条直线,即可判断出正误;
⑤利用线面垂直与平行的性质及其判定定理可知:正确.
解答 解:①若α∩β=a,b?α,a⊥b,则α⊥β不一定成立,可能相交不垂直;
②若a?α,a垂直于β内任意一条直线,则α⊥β,正确;
③若α⊥β,α∩β=a,α∩γ=b,则a⊥b,不一定成立,不正确;
④若a不垂直平面α,则a可能垂直于平面α内的无数条直线,因此不正确;
⑤若a⊥α,b⊥β,a∥b,则α∥β,利用线面垂直与平行的性质及其判定定理可知:正确.
上述五个命题中,正确命题的序号是②⑤.
故选:D.
点评 本题考查了空间位置关系的判定及其性质,考查了空间想象能力、推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}π$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
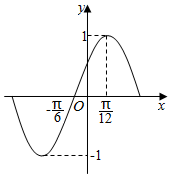 如图是某函数图象的一部分,则该函数表达式是( )
如图是某函数图象的一部分,则该函数表达式是( )| A. | $y=cos(\frac{π}{6}-2x)$ | B. | $y=cos(2x-\frac{π}{3})$ | C. | $y=sin(x+\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com