
分析 (1)由题意和正弦定理以及同角三角函数基本关系可得tanB,可得B值,再由正弦定理整体可得ac的值,代入三角形的面积公式计算可得;
(2)由余弦定理可得c值,在△ABD中由余弦定理可得.
解答 解:(1)∵在△ABC中$ccosB=\sqrt{3}bsinC$,
∴由正弦定理可得sinCcosB=$\sqrt{3}$sinBsinC,
约掉sinC可得cosB=$\sqrt{3}$sinB,
∴tanB=$\frac{sinB}{cosB}$=$\frac{\sqrt{3}}{3}$,B=$\frac{π}{6}$,
又∵${a^2}sinC=4\sqrt{3}sinA$,
∴a2c=4$\sqrt{3}$a,∴ac=4$\sqrt{3}$,
∴△ABC的面积S=$\frac{1}{2}$acsinB=$\sqrt{3}$;
(2)∵$a=2\sqrt{3}$,$b=\sqrt{7}$,
∴由余弦定理可得7=12+c2-2×2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$c,
解关于c的方程可得c=5,或c=1(不满足c>b,舍去)
∵BC边的中点为D,∴在△ABD中由余弦定理可得:
AD2=($\sqrt{3}$)2+52-2×$\sqrt{3}$×5×$\frac{\sqrt{3}}{2}$=13,
开方可得AD的长为$\sqrt{13}$.
点评 本题考查正余弦定理解三角形,涉及整体法和三角形的面积公式,属中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
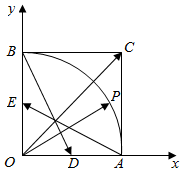 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )| A. | -$\sqrt{2}$ | B. | -2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②④⑤ | C. | ④⑤ | D. | ②⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向右平移$\frac{5π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{5π}{6}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com