
分析 (1)长为x米,宽为y米,则40x+90y+20xy=3200,可得函数y=f(x)的解析式;
(2)由40x+90y≥120$\sqrt{xy}$,得$\sqrt{xy}$的取值范围,即S=xy的取值范围;由40x=90y,且xy=100,解得x,y的值即可.
解答 解:(1)由题意,知:40x+2y×45+20xy=3200,
所以y=$\frac{320-4x}{9+2x}$(0<x<80);
(2)因为40x+90y≥120$\sqrt{xy}$(当且仅当40x=90y时取“=”),
所以:3200≥120$\sqrt{xy}$+20xy,
所以,0<$\sqrt{xy}$≤10;
所以,S=xy≤100.
当40x=90y时,S取最大值,又xy=100,
所以x=15,y=$\frac{20}{3}$,
所以,此时正面铁栅应设计为15米.
点评 本题考查了长方体模型的应用,在求面积S=xy最值时,利用基本不等式是关键.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
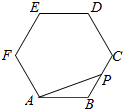 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com