已知a∈R,函数f(x)=x2|x-a|.
(1)当a=2时,求使f(x)=x成立的x的集合;
(2)求函数y=f(x)在区间[1,2]上的最小值.
解:(Ⅰ)由题意,f(x)=x
2|x-2|
当x<2时,由f(x)=x
2(2-x)=x,解得x=0或x=1;
当x≥2时,由f(x)=x
2(x-2)=x,解得x=1+

.
综上,所求解集为{0,1,1+

}
(Ⅱ)设此最小值为m.
①当a≤1时,在区间[1,2]上,f(x)=x
3-ax
2,
∵f′(x)=3x
2-2ax=3x(x-

a)>0,x∈(1,2),
则f(x)是区间[1,2]上的增函数,∴m=f(1)=1-a.
②当1<a≤2时,在区间[1,2]上,f(x)=x
2|x-a|≥0,由f(a)=0知m=f(a)=0.
③当a>2时,在区间[1,2]上,f(x)=ax
2-x
3
f′(x)=2ax-3x
2=3x(

a-x).
若a≥3,在区间(1,2)上,f'(x)>0,则f(x)是区间[1,2]上的增函数,
∴m=f(1)=a-1.
若2<a<3,则1<

a<2.
当1<x<

a时,f'(x)>0,则f(x)是区间[1,

a]上的增函数,
当

a<x<2时,f'(x)<0,则f(x)是区间[

a,2]上的减函数,
因此当2<a<3时,故m=f(1)=a-1或m=f(2)=4(a-2).
当2<a≤

时,4(a-2)≤a-1,故m=f(2)=4(a-2),
当

<a<3时,4(a-2)<a-1,故m=f(1)=a-1.
总上所述,所求函数的最小值m=
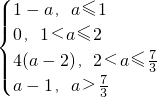
.
分析:(Ⅰ)把a=2代入函数解析式,根据绝对值的符号分为两种情况,即x<2和x≥2分别求解对应方程得根,再把所有的根用列举法表示出来.
(Ⅱ)根据区间[1,2]和绝对值内的式子进行分类讨论,即a≤1、1<a≤2和a≥3三种情况,分别求出解析式和它的导函数,利用导函数的符号判断在闭区间上的单调性,再求最小值;当a≥3时最小值可能取在区间的两端,再通过作差和分类进行比较两个函数值的大小,最后用分段函数表示函数的最小值.
点评:本题主要用了分类讨论的思想解决含有参数的函数求值和求最值问题,分类的标准是绝对值的符号,求闭区间上的最值时,通常是求函数的导数用它的符号判断函数在区间上的单调性,再求最值,有时需要对端点处的函数值进行作差比较大小.

 .
. }
} a)>0,x∈(1,2),
a)>0,x∈(1,2), a-x).
a-x). a<2.
a<2. a时,f'(x)>0,则f(x)是区间[1,
a时,f'(x)>0,则f(x)是区间[1, a]上的增函数,
a]上的增函数, a<x<2时,f'(x)<0,则f(x)是区间[
a<x<2时,f'(x)<0,则f(x)是区间[ a,2]上的减函数,
a,2]上的减函数, 时,4(a-2)≤a-1,故m=f(2)=4(a-2),
时,4(a-2)≤a-1,故m=f(2)=4(a-2), <a<3时,4(a-2)<a-1,故m=f(1)=a-1.
<a<3时,4(a-2)<a-1,故m=f(1)=a-1.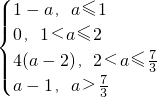 .
.
