
(13分)已知![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,
, ![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)当n取何值时,![]() 取最大值,并求出最大值;
取最大值,并求出最大值;
(III)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解析:(I)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
即![]() .
.
又![]() ,可知对任何
,可知对任何![]() ,
,![]() ,
,
所以![]() .……………………………2分
.……………………………2分
∵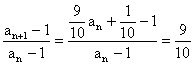 ,
,
∴![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.………4分
的等比数列.………4分
(II)由(I)可知![]() =
=![]() (
(![]() ).
).
∴![]() .
.
 .……………………………5分
.……………………………5分
当n=7时,![]() ,
,![]() ;
;
当n<7时,![]() ,
,![]() ;
;
当n>7时,![]() ,
,![]() .
.
∴当n=7或n=8时,![]() 取最大值,最大值为
取最大值,最大值为![]() .……8分
.……8分
(III)由![]() ,得
,得![]() (*)
(*)
依题意(*)式对任意![]() 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.…………9分
②当t<0时,由![]() ,可知
,可知![]() (
(![]() ).
).
而当m是偶数时![]() ,因此t<0不合题意.…………10分
,因此t<0不合题意.…………10分
③当t>0时,由![]() (
(![]() ),
),
∴![]() ∴
∴![]() . (
. (![]() )……11分
)……11分
设![]() (
(![]() )
)
∵![]() =
=![]() ,
,
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(本小题满分13分)已知函数f (x)=2n![]() 在[0,+
在[0,+![]() 上最小值是a
上最小值是a![]() (n∈N*).
(n∈N*).
(1)求数列{a![]() }的通项公式;(2)已知数列{b
}的通项公式;(2)已知数列{b![]() }中,对任意n∈N*都有b
}中,对任意n∈N*都有b![]() a
a![]() =1成立,设S
=1成立,设S![]() 为数列{b
为数列{b![]() }的前n项和,证明:2S
}的前n项和,证明:2S![]() <1;(3)在点列A
<1;(3)在点列A![]() (2n,a
(2n,a![]() )中是否存在两点A
)中是否存在两点A![]() ,A
,A![]() (i,j∈N*),使直线A
(i,j∈N*),使直线A![]() A
A![]() 的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
查看答案和解析>>
科目:高中数学 来源:2011届福建省厦门外国语学校高三上学期11月月考理科数学卷 题型:解答题
(本小题满分13分)已知数列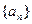 ,定义其倒均数是
,定义其倒均数是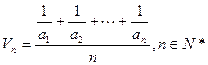 。
。
(1)求数列{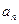 }的倒均数是
}的倒均数是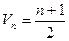 ,求数列{
,求数列{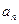 }的通项公式
}的通项公式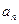 ;
;
(2)设等比数列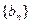 的首项为-1,公比为
的首项为-1,公比为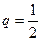 ,其倒数均为
,其倒数均为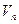 ,若存在正整数k,使
,若存在正整数k,使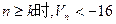 恒成立,试求k的最小值。
恒成立,试求k的最小值。
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上学期期末考试文科数学卷(解析版) 题型:解答题
(本小题13分)已知关于x的一元二次函数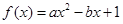 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列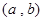 。
。
(1)若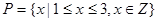 ,
,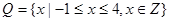 ,列举出所有的数对
,列举出所有的数对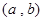 ,并求函数
,并求函数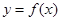 有零点的概率;
有零点的概率;
(2)若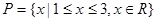 ,
,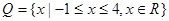 ,求函数
,求函数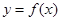 在区间
在区间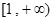 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市西城区高三上学期期末考试文科数学试卷 题型:解答题
(本小题满分13分)已知数列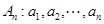 .如果数列
.如果数列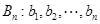 满足
满足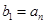 ,
,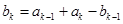 ,其中
,其中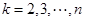 ,则称
,则称 为
为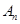 的“衍生数列”.
的“衍生数列”.
(Ⅰ)写出数列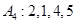 的“衍生数列”
的“衍生数列”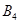 ;
;
(Ⅱ)若 为偶数,且
为偶数,且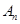 的“衍生数列”是
的“衍生数列”是 ,证明:
,证明: ;
;
(Ⅲ)若 为奇数,且
为奇数,且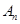 的“衍生数列”是
的“衍生数列”是 ,
, 的“衍生数列”是
的“衍生数列”是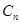 ,….依次将数
,….依次将数
列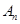 ,
, ,
,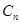 ,…的首项取出,构成数列
,…的首项取出,构成数列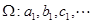 .证明:
.证明: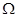 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com