
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
分析 先利用点到直线的距离,求得圆心到直线x0x+y0y=R2的距离,根据P在圆内,判断出,$\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}$<R,进而可知d>R,故可知直线和圆相离.
解答 解:圆心O(0,0)到直线x0x+y0y=R2的距离为d=$\frac{{R}^{2}}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}$,
∵点P(x0,y0)在圆内,∴$\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}$<R,则有d>R,
故直线和圆相离.
故选:C.
点评 本题的考点是直线与圆的位置关系,主要考查了直线与圆的位置关系.直线与圆的位置关系的判定.解题的关键是看圆心到直线的距离与圆的半径的大小关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知⊙O:x2+y2=1和定点A(2,1),⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知⊙O:x2+y2=1和定点A(2,1),⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
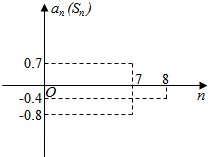 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
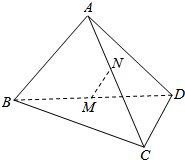 如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.
如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com