
分析 (Ⅰ)运用离心率公式和点满足椭圆方程,解方程可得a,b,即可得到椭圆方程;
(Ⅱ)设M(x1,y1),N(x2,y2),△F1MN的内切圆半径为r,运用等积法和韦达定理,弦长公式,结合基本不等式即可求得最大值.
解答 解:(Ⅰ)由题意得$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,
解得a=2,b=$\sqrt{3}$,c=1,
椭圆C的标准方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)设M(x1,y1),N(x2,y2),△F1MN的内切圆半径为r,
则${S}_{△{F}_{1}MN}$=$\frac{1}{2}$(|MN|+|MF1|+|NF1|)r=$\frac{1}{2}$×8r=4r,
所以要使S取最大值,只需${S}_{△{F}_{1}MN}$最大,
则${S}_{△{F}_{1}MN}$=$\frac{1}{2}$|F1F2|•|y1-y2|=|y1-y2|,
设直线l的方程为x=ty+1,
将x=ty+1代入$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
可得(3t2+4)y2+6ty-9=0(*)
∵△>0恒成立,方程(*)恒有解,
y1+y2=$\frac{-6t}{4+3{t}^{2}}$,y1y2=$\frac{-9}{4+3{t}^{2}}$,
${S}_{△{F}_{1}MN}$=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{12\sqrt{1+{t}^{2}}}{4+3{t}^{2}}$,
记m=$\sqrt{1+{t}^{2}}$(m≥1),
${S}_{△{F}_{1}MN}$=$\frac{12m}{3{m}^{2}+1}$=$\frac{12}{3m+\frac{1}{m}}$在[1,+∞)上递减,
当m=1即t=0时,(${S}_{△{F}_{1}MN}$)max=3,
此时l:x=1,Smax=$\frac{9}{16}$π.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用韦达定理和三角形的面积公式,考查运算能力,属于中档题.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在平面直角坐标系 中,动点
中,动点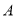 的坐标为
的坐标为 ,其中
,其中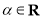 .在极坐标系(以原点
.在极坐标系(以原点 为极点,以
为极点,以 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线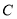 的方程为
的方程为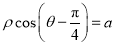 .
.
(Ⅰ)判断动点 的轨迹的形状;
的轨迹的形状;
(Ⅱ)若直线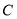 与动点
与动点 的轨迹有且仅有一个公共点,求实数
的轨迹有且仅有一个公共点,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
已知命题 :若
:若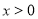 ,则函数
,则函数 的最小值为
的最小值为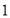 ;命题
;命题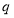 :若
:若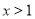 ,则
,则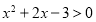 .则
.则
下列命题是真命题的是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
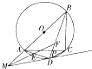 如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.
如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com