
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
分析 依题意,利用和的立方公式可得a7+a2006=2,再利用等差数列的求和公式可得S2012=2012;令f(x)=x3+2012x,利用导数易知y=f(x)为R上的增函数,从而可得f(a7-1)>f(a2006-1),即a7>a2006,故等差数列{an}为递减数列,于是可得答案.
解答 解:∵(a7-1)3+2012(a7-1)=1,(a2006-1)3+2012(a2006-1)=-1,
∴(a7-1)3+(a2006-1)3+2012(a7-1)+2012(a2006-1)=0,
即[(a7-1)+(a2006-1)][(a7-1)2+(a2006-1)2-(a7-1)(a2006-1)]+2012[(a7-1)+(a2006-1)]=0,
整理得:[(a7-1)+(a2006-1)]{[(a7-1)-$\frac{1}{2}$(a2006-1)]2+$\frac{3}{4}$(a2006-1)2+2012]}=0,
∴(a7-1)+(a2006-1)=0,即a7+a2006=2.
∵数列{an}为等差数列,其前n项和为Sn,
∴S2012=$\frac{({a}_{1}+{a}_{2012})×2012}{2}$=$\frac{({a}_{7}+{a}_{2006})×2012}{2}$=2012,可排除A、C;
令f(x)=x3+2012x,则f′(x)=3x2+2012>0,
∴y=f(x)为R上的增函数,又f(a7-1)=1>-1=f(a2006-1),
∴a7-1>a2006-1,即a7>a2006,故等差数列{an}为递减数列,
∴a7>a2012,可排除B,
故选:D.
点评 本题考查数列递推关系式的应用,考查构造函数思想及利用导数法判断函数的单调性,求得a7+a2006=2及等差数列{an}为递减数列是关键,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
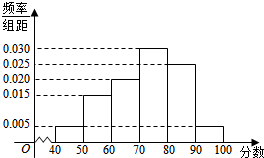 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com