
分析 (I)通过已知条件及正弦定理可得CB+CA=2λ(定值)且2λ>2,由椭圆的定义计算即可;
(II)当λ=$\sqrt{3}$时,椭圆方程为$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1(x≠±$\sqrt{3}$).分过定点B(1,0)的直线与x轴重合与不重合两种情况讨论.对于过定点B(1,0)的直线不与x轴重合时,通过
设l方程,并与椭圆联立,利用韦达定理及点到直线的距离公式、三角形面积公式、换元法以及函数的单调性,计算即可.
解答 解:(I)在△ABC中,根据正弦定理,
可得$\frac{sinA+sinB}{sinC}$=$\frac{CB+CA}{AB}$,即$\frac{CB+CA}{AB}$=λ,
∵AB=2,∴CB+CA=2λ(定值),且2λ>2,
∴动点C的轨迹方程i为椭圆(除去与A、B共线的两个点),
设其标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
∴a2=λ2,b2=λ2-1,
∴所求曲线的轨迹方程为:$\frac{{x}^{2}}{{λ}^{2}}$+$\frac{{y}^{2}}{{λ}^{2}-1}$=1(x≠±λ);
(II)当λ=$\sqrt{3}$时,椭圆方程为$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1(x≠±$\sqrt{3}$).
①过定点B(1,0)的直线与x轴重合时,△NPQ面积无最大值;
②过定点B(1,0)的直线不与x轴重合时,
设l方程为:x=my+1,P(x1,y1),Q(x2,y2),
若m=0,∵x≠±$\sqrt{3}$,∴此时△NPQ面积无最大值;
根据椭圆的几何性质,不妨设m>0,
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去x整理得:(2m2+3)y2+4my-4=0,
由韦达定理,得y1+y2=-$\frac{4m}{3+2{m}^{2}}$,y1y2=-$\frac{4}{3+2{m}^{2}}$,
∴|PQ|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\frac{4\sqrt{3}(1+{m}^{2})}{3+2{m}^{2}}$.
联立$\left\{\begin{array}{l}{x=my+n}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y整理得:(3+2m2)y2+4mny+2n2-6=0,
由△=(4mn)2-4(3+2m2)(2n2-6)=0,解得n2=2m2+3(n<-$\sqrt{3}$),
又点N到直线l的距离d=$\frac{|n-1|}{\sqrt{1+{m}^{2}}}$,
∴S△PMN=$\frac{1}{2}•$d•|PQ|=$\frac{1}{2}×$$\frac{|n-1|}{\sqrt{1+{m}^{2}}}$×$\frac{2\sqrt{3}(1+{m}^{2})}{3+2{m}^{2}}$=$\frac{2\sqrt{3}|n-1|\sqrt{1+{m}^{2}}}{3+2{m}^{2}}$,
∴S2=$\frac{12(n-1)^{2}(1+{m}^{2})}{(3+2{m}^{2})^{2}}$,
将n2=2m2+3代入,得S2=6(1-$\frac{1}{n}$)2(1-$\frac{1}{{n}^{2}}$),
令t=$\frac{1}{n}$∈(-$\frac{\sqrt{3}}{3}$,0),设函数f(t)=6(1-t)2(1-t2),
则f′(t)=-12(t-1)2(2t+1),
∵当t∈(-$\frac{\sqrt{3}}{3}$,-$\frac{1}{2}$)时f′(t)>0,当t∈(-$\frac{1}{2}$,0)时f′(t)<0,
∴f(t)在(-$\frac{\sqrt{3}}{3}$,-$\frac{1}{2}$)上是增函数,在(-$\frac{1}{2}$,0)上是减函数,
∴f(t)min=$f(-\frac{1}{2})$=$\frac{81}{8}$,
故m2=$\frac{1}{2}$时,△NPQ的面积最大值是$\frac{9\sqrt{2}}{4}$.
点评 本题是一道直线与圆锥曲线的综合题,考查求椭圆的方程、三角形的面积最大值,考查分类讨论的思想、考查计算求解能力,涉及到韦达定理、点到直线的距离公式、三角形面积公式、换元法以及函数的单调性等知识,注意解题方法的积累,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:选择题
等差数列 中,
中, ,那么关于
,那么关于 的方程:
的方程: ( )
( )
A.无实根 B.有两个相等实根
C.有两个不相等实根 D.不能确定有无实根
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:解答题
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
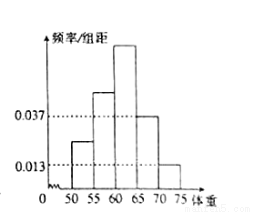
(Ⅰ)求该校高三毕业班想参军的学生人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省高三毕业班想参军的同学中(人数很多)任选三人,设 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.
已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,m∥n,则n∥α | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥α,n?α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
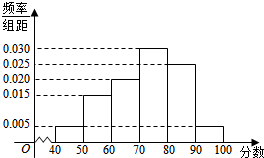 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com