
【题目】某学校为了解高一新生的体能情况,在入学后不久,组织了一次体能测试,按成绩分为优秀、良好、一般、较差四个档次.现随机抽取120名学生的成绩,其条形图如下:
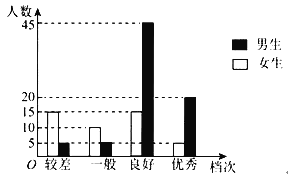
(1)将优秀、良好、一般归为合格,较差归为不合格,试根据条形图完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为学生的成绩与性别有关.
合格 | 不合格 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)学校为了解学生以前参加课外活动的情况,利用分层抽样的方法从120名学生中抽取24名学生参加一个座谈会.
①座谈会上抽取2名学生汇报以前参加课外活动的情况,求恰好抽到测试成绩一个优秀与一个较差的学生的概率;
②为全面提高学生的体能,学校专门安排专职教师对全校测试成绩较差的学生在课外活动时进行专项训练,通过一段时间的训陈后,测试合格率达到了![]() .若某班有4名学生参加这个专项训陈,求训练后测试合格人数ξ的分布列与数学期望.
.若某班有4名学生参加这个专项训陈,求训练后测试合格人数ξ的分布列与数学期望.
附:K2![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(1)列联表见解析,能在犯错误的概率不超过0.01的前提下认为学生的成绩与性别有关;(2)①![]() ,②分布列见解析,
,②分布列见解析,![]()
【解析】
(1)计算观测值,结合临界值表可得;
(2)①由条形图可知:优秀:良好:一般:较差=5:12:3:4,所以从120名学生中抽取24人,其中优秀抽取5人,良好抽取12人,一般抽取3人,较差抽取4人.所以恰好抽到测试成绩一个优秀与一个较差的学生的概率![]() ; ②依题意测试合格人数ξ服从二项分布,即
; ②依题意测试合格人数ξ服从二项分布,即![]() ,根据二项分布的概率公式可得分布列和数学期望.
,根据二项分布的概率公式可得分布列和数学期望.
(1)列联表如下:
合格 | 不合格 | 合计 | |
男生 | 70 | 5 | 75 |
女生 | 30 | 15 | 45 |
合计 | 100 | 20 | 120 |
k2![]() 14.4,
14.4,
∵14.4>6.635,
∴能在犯错误的概率不超过0.01的前提下认为学生的成绩与性别有关
(2)由条形图可知:优秀:良好:一般:较差=25:60:15:20=5:12:3:4,
所以从120名学生中抽取24人,其中优秀抽取5人,良好抽取12人,一般抽取3人,较差抽取4人.
①所以恰好抽到测试成绩一个优秀与一个较差的学生的概率![]() .
.
②依题意测试合格人数ξ服从二项分布,即ξ~B(4,![]() ),∴
),∴
∴P(ξ=0)![]() 0
0![]() 1
1![]() 4
4![]() ,
,
P(ξ=1)![]() 3
3![]() ,
,
P(ξ=2)![]() 2
2![]() 2
2![]() ,
,
P(ξ=3)![]() 3
3![]() ,
,
P(ξ=4)![]() 4
4![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
E(ξ)=0![]() 1
1![]() 2
2![]() 3
3![]() 4
4![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),P是曲线C上的点且对应的参数为
为参数),P是曲线C上的点且对应的参数为![]() ,
,![]() .直线l过点P且倾斜角为
.直线l过点P且倾斜角为![]() .
.
(1)求曲线C的普通方程和直线l的参数方程.
(2)已知直线l与x轴,y轴分别交于![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为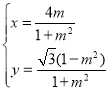 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 上的点到
上的点到![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且a1+a3=30,2S2是3S1和S3的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足![]() ,求数列{bn}前n项和Tn.
,求数列{bn}前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
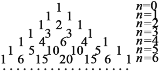
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中曲线
中曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程以及直线
的普通方程以及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)将曲线![]() 向左平移2个单位,再将曲线
向左平移2个单位,再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】超级细菌是一种耐药性细菌,产生超级细菌的主要原因是用于抵抗细菌侵蚀的药物越来越多,但是由于滥用抗生素的现象不断的发生,很多致病菌也对相应的抗生素产生了耐药性,更可怕的是,抗生素药物对它起不到什么作用,病人会因为感染而引起可怕的炎症,高烧,痉挛,昏迷,甚至死亡.
某药物研究所为筛查某种超级细菌,需要检验血液是否为阳性,现有![]() 份血液样本,每个样本取到的可能性相等,有以下两种检验方式:(1)逐份检验,则需要检验
份血液样本,每个样本取到的可能性相等,有以下两种检验方式:(1)逐份检验,则需要检验![]() 次;(2)混合检验,将其中
次;(2)混合检验,将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,则这
)份血液样本分别取样混合在一起检验,若检验结果为阴性,则这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为
份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]()
现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]()
(1)运用概率统计的知识,若![]() ,试求关于
,试求关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)若![]() 与抗生素计量
与抗生素计量![]() 相关,其中
相关,其中![]() 是不同的正实数,满足
是不同的正实数,满足![]() ,对任意的
,对任意的![]() ,都有
,都有![]()
(i)证明:![]() 为等比数列;
为等比数列;
(ii)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com