
【题目】非空集合G关于运算⊕满足:
(1)对任意a,b∈G,都有a+b∈G;
(2)存在e∈G使得对于一切a∈G都有a⊕e=e⊕a=a,
则称G是关于运算⊕的融洽集,
现有下列集合与运算:
①G是非负整数集,⊕:实数的加法;
②G是偶数集,⊕:实数的乘法;
③G是所有二次三项式构成的集合,⊕:多项式的乘法;
④G={x|x=a+b ![]() ,a,b∈Q},⊕:实数的乘法;
,a,b∈Q},⊕:实数的乘法;
其中属于融洽集的是(请填写编号)
【答案】①④
【解析】解:①对于任意非负整数a,b知道:a+b仍为非负整数,所以a⊕b∈G;取e=0,及任意非负整数a,则a+0=0+a=a,因此G对于⊕为整数的加法运算来说是“融洽集”;
②对于任意偶数a,b知道:a+b仍为偶数,故有a+b∈G;但是不存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,故②的G不是“融洽集”.
③对于G={二次三项式},若a、b∈G时,a,b的两个同类项系数,则其积不再为二次三项式,故G不是和谐集,故③不正确;
④G={x|x=a+b ![]() ,a,b∈Q},设x1=a+b
,a,b∈Q},设x1=a+b ![]() ,x2=c+d
,x2=c+d ![]() ,则设x1+x2=(a+c)+(b+d)
,则设x1+x2=(a+c)+(b+d) ![]() ,属于集合G,
,属于集合G,
取e=1,a×1=1×a=a,因此G对于⊕实数的乘法运算来说是“融洽集”,故④中的G是“融洽集”.
故答案为①④.
逐一验证几个选项是否分别满足“融洽集”的两个条件,若两个条件都满足,是“融洽集”,有一个不满足,则不是“融洽集”.


科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2﹣x﹣1在(﹣∞,+∞)上是单调函数,则实数a的取值范围是( )
A.[﹣![]() ,
, ![]() ]
]
B.(﹣![]() ,
, ![]() )
)
C.(﹣∞,﹣![]() )∪(
)∪(![]() , +∞)
, +∞)
D.(﹣∞,﹣![]() )∩(
)∩(![]() , +∞)
, +∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们教材中利用该图作为“( )”的几何解释. 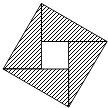
A.如果a>b,b>c,那么a>c
B.如果a>b>0,那么a2>b2
C.对任意实数a和b,有a2+b2≥2ab,当且仅当a=b时等号成立
D.如果a>b,c>0那么ac>bc
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题甲:关于x的不等式x2+(a﹣1)x+a2≤0的解集为空集;命题乙:方程x2+ ![]() ax﹣(a﹣4)=0有两个不相等的实根.
ax﹣(a﹣4)=0有两个不相等的实根.
(1)若甲,乙都是真命题,求实数a的取值范围;
(2)若甲,乙中有且只有一个是假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈(﹣∞,0),2x<3x;命题q:x∈(0,![]() ),tanx>sinx,则下列命题为真命题的是( )
),tanx>sinx,则下列命题为真命题的是( )
A.p∧q
B.p∨(﹁q)
C.(﹁p)∧q
D.p∧(﹁q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com