
分析 由条件利用同角三角函数的基本关系、正弦定理,把角的关系转化为边的关系可得c2=2ab•cosC,再利用余弦定理求得要求式子的值.
解答 解:△ABC中,∵tanAtanC+tanBtanC=2tanAtanB,即 $\frac{sinAsinC}{cosAcosC}$+$\frac{sinBsinC}{cosBcosC}$=2$\frac{sinAsinB}{cosAcosB}$,
即 $\frac{sinC(sinAcosB+cosAsinB)}{cosAcosBcosC}$=2$\frac{sinAsinB}{cosAcosB}$,即 $\frac{sinC•sin(A+B)}{cosC}$=2sinAsinB,即 sin2C=2sinAsinBcosC.
∴c2=2ab•cosC=2ab•$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=a2+b2-c2,即 2c2=a2+b2,∴$\frac{{{a^2}+{b^2}}}{c^2}$=2,
故答案为:2.
点评 本题考查正弦定理,余弦定理的应用,同角三角函数的基本关系、正弦定理,把角的关系转化为边的关系,是解题的关键,属于基础题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:填空题
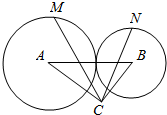 如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].
如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k∈(-3,1) | B. | k∈[-3,1] | C. | k∈(0,1) | D. | k∈(-∞,-3)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com