
���� ��1��������ɵã�$\frac{c}{a}=\frac{\sqrt{2}}{2}$��4a=4$\sqrt{2}$��a2=b2+c2��������ɵó���
��2��F2��0��-1������A��x1��y1����B��x2��y2��.$\overrightarrow{A{F}_{2}}$=$��\overrightarrow{{F}_{2}B}$��$\frac{1}{2}�ܦˡ�$1��-x1=��x2�������ı���PAQB��ƽ���ı��Σ��ɵ�$\overrightarrow{PQ}$=$\overrightarrow{PA}+\overrightarrow{PB}$=��x1+x2��y1+y2+4����
��ֱ��AB�ķ���Ϊ��y=kx-1������Բ����������Ϊ����k2+2��x2-2kx-1=0�����ø���ϵ���Ĺ�ϵ�ɵã�k2=$\frac{-2��1-�ˣ�^{2}}{{��}^{2}-6��+1}$���ɵã�k2��$[0��\frac{2}{7}]$������$|\overrightarrow{PQ}|$=$\sqrt{��{x}_{1}+{x}_{2}��^{2}+��{y}_{1}+{y}_{2}+4��^{2}}$=$\sqrt{16-\frac{28{k}^{2}+48}{{k}^{4}+4{k}^{2}+4}}$����k2=t��$[0��\frac{2}{7}]$��f��t��=$\frac{7t+12}{{t}^{2}+4t+4}$�������õ����о������ĵ����Լ��ɵó���
��� �⣺��1��������ɵã�$\frac{c}{a}=\frac{\sqrt{2}}{2}$��4a=4$\sqrt{2}$��a2=b2+c2�����a=$\sqrt{2}$��b=c=1��
����ԲC�ı�����Ϊ��$\frac{{y}^{2}}{2}+{x}^{2}$=1��
��2��F2��0��-1����
��A��x1��y1����B��x2��y2��.$\overrightarrow{A{F}_{2}}$=$��\overrightarrow{{F}_{2}B}$��$\frac{1}{2}�ܦˡ�$1��
-x1=��x2��
���ı���PAQB��ƽ���ı��Σ�
$\overrightarrow{PQ}$=$\overrightarrow{PA}+\overrightarrow{PB}$=��x1+x2��y1+y2+4����
��ֱ��AB�ķ���Ϊ��y=kx-1��
����$\left\{\begin{array}{l}{y=kx-1}\\{\frac{{y}^{2}}{2}+{x}^{2}=1}\end{array}\right.$��������k2+2��x2-2kx-1=0��
��x1+x2=$\frac{2k}{{k}^{2}+2}$��x1x2=$\frac{-1}{{k}^{2}+2}$��-x1=��x2��
�ɵã�k2=$\frac{-2��1-�ˣ�^{2}}{{��}^{2}-6��+1}$=$\frac{2}{\frac{4}{��+\frac{1}{��}-2}-1}$��
��=1ʱ��k=0��
$�ˡ�[\frac{1}{2}��1��$ʱ��k2��$��0��\frac{2}{7}]$��
���Ͽɵã�k2��$[0��\frac{2}{7}]$��
��y1+y2=kx1-1+kx2-1=k��x1+x2��-2��
��$|\overrightarrow{PQ}|$=$\sqrt{��{x}_{1}+{x}_{2}��^{2}+��{y}_{1}+{y}_{2}+4��^{2}}$
=$\sqrt{��{x}_{1}+{x}_{2}��^{2}+[k��{x}_{1}+{x}_{2}��+2]^{2}}$
=$\sqrt{��\frac{2k}{{k}^{2}+2}��^{2}+��\frac{2{k}^{2}}{{k}^{2}+2}+2��^{2}}$
=$\sqrt{\frac{16{k}^{4}+36{k}^{2}+16}{{k}^{4}+4{k}^{2}+4}}$=$\sqrt{16-\frac{28{k}^{2}+48}{{k}^{4}+4{k}^{2}+4}}$��
��k2=t��$[0��\frac{2}{7}]$��f��t��=$\frac{7t+12}{{t}^{2}+4t+4}$��
f�䣨t��=$\frac{7��{t}^{2}+4t+4��-��7t+12����2t+4��}{��t+2��^{4}}$=$\frac{-��7{t}^{2}+24t+20��}{��t+2��^{4}}$��0��
�ຯ��f��t����t��$[0��\frac{2}{7}]$�ϵ����ݼ�����f��t����$[\frac{343}{128}��3]$��
��$|\overrightarrow{PQ}|$��$[2��\frac{13\sqrt{2}}{8}]$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ�ҳ����⡢���������������ʡ�ƽ���ı��η������õ����о������Ĵ�С��ֵ����ֵ����������������������������������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{2}$ | B�� | 4 | C�� | $��2\sqrt{2}$ | D�� | ��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
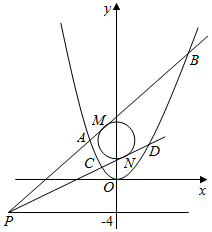 ��ֱ������ϵxOy�У�������C1��x2=4y��ԲC2��x2+��y-5��2=9����P��ֱ��y=-4�ϵĶ��㣮
��ֱ������ϵxOy�У�������C1��x2=4y��ԲC2��x2+��y-5��2=9����P��ֱ��y=-4�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com