
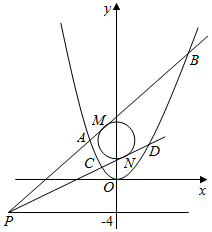
 在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.
在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.分析 (1)求出C2到直线MN的距离,由射影定理可得C2P=30,利用两点间的距离公式求点P的坐标;
(2)当点P在直线y=-4上运动时,设P(x0,-4),切线方程为kx-y-kx0-4=0,所以(x02-9)k2+18x0k+72=0,设过P所作的两条切线PA,PC的斜率分别为k1,k2,则k1+k2=-$\frac{18{x}_{0}}{{{x}_{0}}^{2}-9}$,k1k2=-$\frac{72}{{{x}_{0}}^{2}-9}$,由$\left\{\begin{array}{l}{{k}_{1}x-y-{k}_{1}{x}_{0}-4=0}\\{{x}^{2}=4y}\end{array}\right.$,得x2-4k1x+4(k1x0+4)=0,设四点A、B、C、D的横向联合坐标分别是x1,x2,x3,x4,则x1x2=4(k1x0+4),x3x4=4(k2x0+4),由此能证明四点A,B,C,D的横坐标之积为定值.
解答 解:(1)设P(x,-4),则
∵圆C2:x2+(y-5)2=9,|MN|=$\frac{3\sqrt{91}}{5}$,
∴C2到直线MN的距离为$\sqrt{9-(\frac{1}{2}×\frac{3\sqrt{91}}{5})^{2}}$=$\frac{3}{10}$,
由射影定理可得9=$\frac{3}{10}×{C}_{2}P$,∴C2P=30,
∴$\sqrt{{x}^{2}+81}$=30,∴x=±3$\sqrt{91}$,
∴P(±3$\sqrt{91}$,-4);
(2)当点P在直线y=-4上运动时,设P(x0,-4),
由题意知x0≠±3,过P且于圆C2相切的直线的斜率存在,每条切线都与抛物线有两个交点,
切线方程为y+4=k(x-x0),即kx-y-kx0-4=0,
∴$\frac{|-5-k{x}_{0}-4|}{\sqrt{{k}^{2}+1}}$=3,
整理,得(x02-9)k2+18x0k+72=0,①
设过P所作的两条切线PA,PC的斜率分别为k1,k2,
则k1,k2是方程①的两个实根,
∴k1+k2=-$\frac{18{x}_{0}}{{{x}_{0}}^{2}-9}$,k1k2=-$\frac{72}{{{x}_{0}}^{2}-9}$,②
由$\left\{\begin{array}{l}{{k}_{1}x-y-{k}_{1}{x}_{0}-4=0}\\{{x}^{2}=4y}\end{array}\right.$,得x2-4k1x+4(k1x0+4)=0,③
设四点A、B、C、D的横向联合坐标分别是x1,x2,x3,x4,
则x1,x2是方程③的两个实根,
∴x1x2=4(k1x0+4),④
同理,x3x4=4(k2x0+4),⑤
由②④⑤三式得:
x1x2x3x4=16(k1x0+4)(k2x0+4)
=16[k1k2x02+4x0(k1+k2)+16]
=16($\frac{72{{x}_{0}}^{2}}{{{x}_{0}}^{2}-9}-4{x}_{0}•\frac{18{x}_{0}}{{{x}_{0}}^{2}-9}+16$)
=16×16=256.
∴当点P在直线y=-4上运动时,四点A、B、C、D的横坐标之积为定值256.
点评 本题考查曲线方程的求法,考查四点的横坐标之积为定值的探求,考查韦达定理,知识综合性强,难度大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 108 | B. | 120 | C. | 132 | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
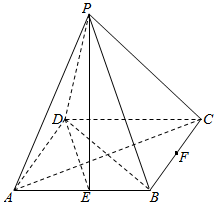 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com