
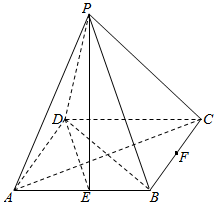
 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.分析 (Ⅰ)由题意和向量法可证AC⊥DE,再由题意和线面垂直的性质可得DE⊥平面PAC;
(Ⅱ)当点M在PC边上且满足$\frac{PM}{MC}$=3时,FM∥平面PDE,作MN∥PD交CD与N,连接NF,可证平面MNF∥平面PDE,由面面平行的性质可得.
解答  (Ⅰ)证明:由题意可得|$\overrightarrow{AB}$|=2$\sqrt{2}$,|$\overrightarrow{AD}$|=2,且$\overrightarrow{AB}$⊥$\overrightarrow{AD}$,
(Ⅰ)证明:由题意可得|$\overrightarrow{AB}$|=2$\sqrt{2}$,|$\overrightarrow{AD}$|=2,且$\overrightarrow{AB}$⊥$\overrightarrow{AD}$,
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,$\overrightarrow{DE}$=$\overrightarrow{AE}$-$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AD}$,
∴$\overrightarrow{AC}$•$\overrightarrow{DE}$=($\overrightarrow{AB}$+$\overrightarrow{AD}$)•($\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AD}$)=$\frac{1}{2}$${\overrightarrow{AB}}^{2}$-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-${\overrightarrow{AD}}^{2}$
=$\frac{1}{2}$${\overrightarrow{AB}}^{2}$-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-${\overrightarrow{AD}}^{2}$=$\frac{1}{2}$×8-0-4=0,
∴$\overrightarrow{AC}$⊥$\overrightarrow{DE}$,即AC⊥DE,又点P在底面上的射影在AC上,
∴平面PAC⊥平面ABCD,又AC为平面PAC与平面ABCD的交线,
DE?平面ABCD,∴DE⊥平面PAC;
(Ⅱ)当点M在PC边上且满足$\frac{PM}{MC}$=3时,FM∥平面PDE,下面证明:
作MN∥PD交CD与N,连接NF,在底面矩形中可证NF∥DE,
由MN∥PD可得MN∥平面PDE,由NF∥DE可得NF∥平面PDE,
再由MN和NF相交可得平面MNF∥平面PDE,
又MF?平面MNF,∴FM∥平面PDE.
点评 本题考查直线和平面平行和垂直的判定,作辅助线是解决问题的关键,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
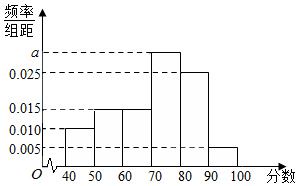 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
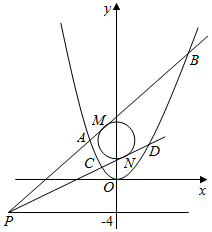 在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.
在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21个 | B. | 25个 | C. | 32个 | D. | 42个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 无数个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com