
分析 (1)设C(-$\frac{p}{2}$,t),过C的切线l的方程为:y-t=k(x+$\frac{p}{2}$),联立抛物线E:y2=2px,消去x,利用△=0,结合韦达定理求k1•k2;
(2)确定直线AB经过焦点F,直线AB的一个方向向量为$\overrightarrow{m}$=(1-k2,2k),证明$\overrightarrow{FC}•\overrightarrow{m}$=0,即可得出结论.
解答 解:(1)设C(-$\frac{p}{2}$,t),过C的切线l的方程为:y-t=k(x+$\frac{p}{2}$),
联立抛物线E:y2=2px,消去x得:ky2-2py+p(2t+pk)=0①
l与E相切时,方程①由两个相等的实根,则△=0,即pk2+2tk-p=0②
方程②的两根k1,k2是切线CA,CB的斜率,由根与系数的关系知:k1k2=-1;
(2)设A(x1,y1),B(x2,y2),CA的斜率为k,则y1是方程①的相等实根,
由根与系数的关系得y1=$\frac{p}{k}$,则x1=$\frac{p}{2{k}^{2}}$.
由题意,CB的斜率为-$\frac{1}{k}$,
同理y2=-pk,则x2=$\frac{p{k}^{2}}{2}$.
∴kAB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{2k}{1-{k}^{2}}$.
直线AB的方程为y+pk=$\frac{2k}{1-{k}^{2}}$(x-$\frac{p{k}^{2}}{2}$).
令y=0,得x=$\frac{p}{2}$,∴直线AB经过焦点F.
由方程②得t=$\frac{p(1-{k}^{2})}{2k}$,则直线AB的一个方向向量为$\overrightarrow{m}$=(1-k2,2k),
$\overrightarrow{FC}$=(-p,$\frac{p(1-{k}^{2})}{2k}$)=$\frac{p}{2k}$(-2k,1-k2),
∴$\overrightarrow{FC}•\overrightarrow{m}$=0,
∴C在AB上的射影为定点F($\frac{p}{2}$,0).
点评 本题考查直线与抛物线的位置关系,考查根与系数的运用,考查学生分析解决问题的能力,属于中档题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
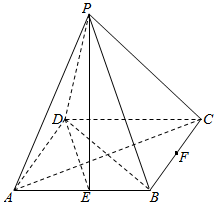 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com