练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    现有一组互不相同且从小到大排列的数据:a0,a1,a2,a3,a4,a5,其中a0=0.为提取反映数据间差异程度的某种指标,今对其进行如下加工:记T=a0+a1+…+a5,xn=,yn=(a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2, …,5)的折线.

    (1)求f(0)和f(1)的值;

    (2)设Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1、k2、k3、k4、k5的大小关系;

    (3)证明当x∈(0,1)时,f(x)＜x.

    思路解析:本题主要考查函数知识、斜率公式、分析问题解决问题的能力,结合已知采用分析法将所求问题转化到能够解决的范围内.

    (1)解:f(0)==0,f(1)==1.

    (2)解:kn=,n=1,2, …,5,

    因为a1＜a2＜a3＜a4＜a5,

    所以k1＜k2＜k3＜k4＜k5.

    (3)证明:由于f(x)的图象是连结各点Pn(xn,yn)(n=0,1, …,5)的折线,要证明f(x)＜x(0＜x＜1),只需证明f(xn)＜xn(n=1,2,3,4).事实上,当x∈(xn-1,xn)时,

    f(x)=(x-xn-1)+f(xn-1)

    =f(xn-1)+f(xn)

    ＜=x.

    下面证明f(xn)＜xn.

    对任何n(n=1,2,3,4),

    5(a1+…+an)=［n+(5-n)］(a1+…+an)

    =n(a1+…+an)+(5-n)(a1+…+an)

    ≤n(a1+…+an)+(5-n)nan=n［a1+…+an+(5-n)an］

    ＜n(a1+…+an+an+1+…+a5)=nT.

    所以f(xn)=＜=xn.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•通州区一模）现有一组互不相同且从小到大排列的数据a0，a1，a2，a3，a4，a5，其中a0=0．记T=a0+a1+a2+a3+a4+a5，xn=
    n
    5
    ，yn=
    1
    T
    (a0+a1+…+an)    （n=0，1，2，3，4，5），作函数y=f（x），使其图象为逐点依次连接点Pn（xn，yn）（n=0，1，2，3，4，5）的折线．
    （Ⅰ）求f（0）和f（1）的值；
    （Ⅱ）设直线Pn-1Pn的斜率为kn（n=1，2，3，4，5），判断k1，k2，k3，k4，k5的大小关系；
    （Ⅲ）证明：当x∈（0，1）时，f（x）＜x．

    查看答案和解析>>

    科目：高中数学 来源：通州区一模 题型：解答题

    现有一组互不相同且从小到大排列的数据a0，a1，a2，a3，a4，a5，其中a0=0．记T=a0+a1+a2+a3+a4+a5，xn=
    n
    5
    ，yn=
    1
    T
    (a0+a1+…+an)    （n=0，1，2，3，4，5），作函数y=f（x），使其图象为逐点依次连接点Pn（xn，yn）（n=0，1，2，3，4，5）的折线．
    （Ⅰ）求f（0）和f（1）的值；
    （Ⅱ）设直线Pn-1Pn的斜率为kn（n=1，2，3，4，5），判断k1，k2，k3，k4，k5的大小关系；
    （Ⅲ）证明：当x∈（0，1）时，f（x）＜x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    20.现有一组互不相同且从小到大排列的数据：a0，a1，a2，a3，a4，a5，其中a0=0.为提取反映数据间差异程度的某种指标，今对其进行如下加工：记T=a0+a1+…a5，xn=，yn=（a0+a1+…+an），作函数y=f（x），使其图像为逐点依次连接点Pn（xn，yn）（n=0，1，2，…，5）的折线.

    （Ⅰ）求f（0）和f（1）的值；

    （Ⅱ）设Pn－1Pn的斜率为kn（n=1，2，3，4，5），判断k1，k2，k3，k4，k5的大小关系；

    （Ⅲ）证明：f（xn）<xn（n=1，2，3，4）.

    查看答案和解析>>

    科目：高中数学 来源：2013年北京市通州区高考数学一模试卷（理科）（解析版） 题型：解答题

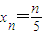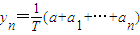    现有一组互不相同且从小到大排列的数据a，a1，a2，a3，a4，a5，其中a=0．记T=a+a1+a2+a3+a4+a5，，（n=0，1，2，3，4，5），作函数y=f（x），使其图象为逐点依次连接点Pn（xn，yn）（n=0，1，2，3，4，5）的折线．
    （Ⅰ）求f（0）和f（1）的值；
    （Ⅱ）设直线Pn-1Pn的斜率为kn（n=1，2，3，4，5），判断k1，k2，k3，k4，k5的大小关系；
    （Ⅲ）证明：当x∈（0，1）时，f（x）＜x．

    查看答案和解析>>

    同步练习册答案