
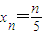 ,
,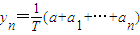 (n=0,1,2,3,4,5),作函数y=f(x),使其图象为逐点依次连接点Pn(xn,yn)(n=0,1,2,3,4,5)的折线.
(n=0,1,2,3,4,5),作函数y=f(x),使其图象为逐点依次连接点Pn(xn,yn)(n=0,1,2,3,4,5)的折线.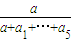 ,f(1)=
,f(1)=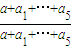 即可求解
即可求解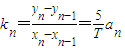 ,结合已知a<a1<a2<a3<a4<a5,可判断
,结合已知a<a1<a2<a3<a4<a5,可判断 ,…(2分)
,…(2分)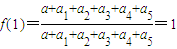 ; …(4分)
; …(4分)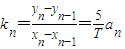 ,n=1,2,3,4,5. …(6分)
,n=1,2,3,4,5. …(6分)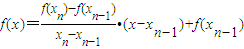 =
=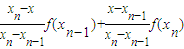
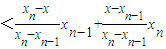 =x.
=x.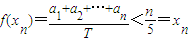 .…(13分)
.…(13分)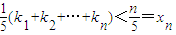 ;…(10分)
;…(10分)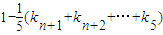
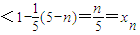 .
.

科目:高中数学 来源: 题型:
| n |
| 5 |
| 1 |
| T |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求f(0)和f(1)的值;
(2)设Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1、k2、k3、k4、k5的大小关系;
(3)证明当x∈(0,1)时,f(x)<x.
查看答案和解析>>
科目:高中数学 来源:通州区一模 题型:解答题
| n |
| 5 |
| 1 |
| T |
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)求f(0)和f(1)的值;
(Ⅱ)设Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1,k2,k3,k4,k5的大小关系;
(Ⅲ)证明:f(xn)<xn(n=1,2,3,4).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com