
【题目】四棱柱![]() 的底面是菱形,
的底面是菱形,![]() 平面
平面![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的点
上的点![]()
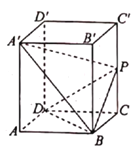
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求四棱锥
的中点,求四棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
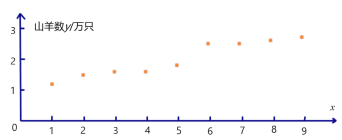
【题目】某县畜牧技术员张三和李四![]() 年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量
年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() (单位:万只)与相应年份
(单位:万只)与相应年份![]() (序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
年份序号 |
|
|
|
|
|
|
|
|
|
年养殖山羊 |
|
|
|
|
|
|
|
|
|
(1)根据表中的数据和所给统计量,求![]() 关于
关于![]() 的线性回归方程(参考统计量:
的线性回归方程(参考统计量:![]() ,
,![]() ;
;
(2)李四提供了该县山羊养殖场的个数![]() (单位:个)关于
(单位:个)关于![]() 的回归方程
的回归方程![]() .
.
试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:![]()
![]()
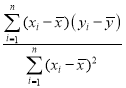 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
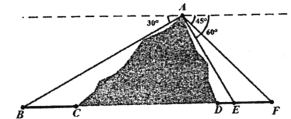
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 的距离与它到直线
的距离与它到直线![]() 的距离
的距离![]() 的比值为
的比值为![]() ,设动点
,设动点![]() 形成的轨迹为曲线
形成的轨迹为曲线![]() ..
..
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,过
两点,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为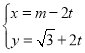 (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为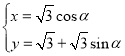 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求曲线
轴正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
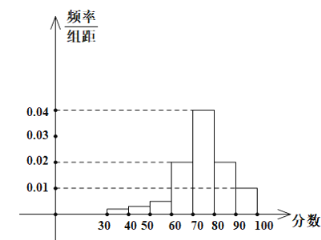
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车因绿色、环保、健康的出行方式,在国内得到迅速推广.最近,某机构在某地区随机采访了10名男士和10名女士,结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”,其他人表示“较少或不选择骑共享单车出行”.
(1)从这些男士和女士中各抽取一人,求至少有一人“经常骑共享单车出行”的概率;
(2)从这些男士中抽取一人,女士中抽取两人,记这三人中“经常骑共享单车出行”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com