
| A. | [1,+∞) | B. | (-∞,-1] | C. | [1,0) | D. | (0,1] |
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | A=30°.B=45°.c=10 | B. | a=$\sqrt{3}$.c=$\sqrt{2}$.B=45° | ||
| C. | a=14.c=16.A=45° | D. | c=7.b=5.C=80° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4,5} | B. | {1,4} | C. | {1,2,4} | D. | {3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
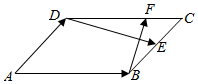 如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;
如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com