
【题目】海安市江淮文化园是以江淮历史文化为底蕴的人文景观,整个园区由白龙故里、先贤景区、凤山书院、中国名人艺术馆群四大景区组成.据估计,其中凤山书院景区每天的水电、人工等固定成本为1000元,另每增加一名游客需另外增加成本10元,凤山书院景区门票单价x(元)(x∈N*)与日门票销售量![]() (张)的关系如下表,并保证凤山书院景区每天盈利.
(张)的关系如下表,并保证凤山书院景区每天盈利.
x | 20 | 35 | 40 | 50 |
y | 400 | 250 | 200 | 100 |
(1)在坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定y与x的函数关系式;
的对应点,并确定y与x的函数关系式;
(2)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(3)请写出凤山书院景区的日利润![]() 的表达式,并回答该景区怎样定价才能获最大日利润?
的表达式,并回答该景区怎样定价才能获最大日利润?
【答案】(1)![]()
![]()
![]() ; (2)销售单价每上涨1元,日销售量减少10张;(3)
; (2)销售单价每上涨1元,日销售量减少10张;(3)![]() (
(![]() N*),当
N*),当![]() 时,
时,![]() 有最大值
有最大值![]() ,故单价定为
,故单价定为![]() 元时,才能获得日最大利润.
元时,才能获得日最大利润.
【解析】
(1)由题表作出四点的对应点,它们分布在一条直线上,据此可得函数解析式为![]() (
(![]() N*).
N*).
(2)由(1)可得![]() ,然后解释其实际意义即可;
,然后解释其实际意义即可;
(3)由题意求得函数![]() 的解析式,然后结合二次函数的性质讨论该景区怎样定价才能获最大日利润即可.
的解析式,然后结合二次函数的性质讨论该景区怎样定价才能获最大日利润即可.
(1)由题表在坐标纸中作出四点的对应点如图所示,它们分布在一条直线上,
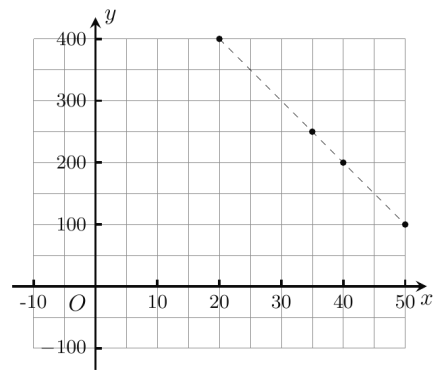
设它们共线于![]() ,则取两点
,则取两点![]() 的坐标代入得:
的坐标代入得:
![]() .
.
所以![]() (
(![]() N*),
N*),
经检验![]() ,也在此直线上.
,也在此直线上.
故所求函数解析式为![]() (
(![]() N*).
N*).
(2)由(1)可得![]() ,实际意义表示:销售单价每上涨1元,日销售量减少10张.
,实际意义表示:销售单价每上涨1元,日销售量减少10张.
(3)依题意:![]() (
(![]() N*)图象开口向下,对称轴为
N*)图象开口向下,对称轴为![]() .
.
当![]() 时,函数单调递增;当
时,函数单调递增;当![]() 时,函数单调递减. 故当
时,函数单调递减. 故当![]() 时,
时,![]() 有最大值
有最大值![]() ,答:当
,答:当![]() 时,
时,![]() 有最大值
有最大值![]() ,故单价定为
,故单价定为![]() 元时,才能获得日最大利润.
元时,才能获得日最大利润.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() ,点
,点![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的倾斜角分别为
的倾斜角分别为![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x)的图象关于点 ![]() 成中心对称,对任意的实数x都有f(x)=﹣f(x+
成中心对称,对任意的实数x都有f(x)=﹣f(x+ ![]() ),且f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+f(3)+…+f(2014)的值为( )
),且f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+f(3)+…+f(2014)的值为( )
A.2
B.1
C.﹣1
D.﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=4x2-2(t-2)x-2t2-t+1在区间[-1,1]内至少存在一个值m,使得f(m)>0,则实数t的取值范围( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣|x|+2a﹣1(a为实常数).
(1)若a=1,求f(x)=3的解;
(2)求f(x)在区间[1,2]的最小值为g(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为R,且满足
(1)f(1)=3
(2)对于任意的![]() ,总有
,总有![]()
(3)对于任意的![]()
(I)求f(0)及f(-1)的值
(II)求证:函数y=f(x)-1为奇函数
(III)若![]() ,求实数m的取值范围
,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( ) 
A.(kπ﹣ ![]() ,kπ+
,kπ+ ![]() ,),k∈z
,),k∈z
B.(2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ),k∈z
),k∈z
C.(k﹣ ![]() ,k+
,k+ ![]() ),k∈z
),k∈z
D.( ![]() ,2k+
,2k+ ![]() ),k∈z
),k∈z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列{an},若an+2﹣an=d(d是与n无关的常数,n∈N*),则称数列{an}叫做“弱等差数列”,已知数列{an}满足:a1=t,a2=s且an+an+1=an+b对于n∈N*恒成立,(其中t,s,a,b都是常数).
(1)求证:数列{an}是“弱等差数列”,并求出数列{an}的通项公式;
(2)当t=1,s=3时,若数列{an}是等差数列,求出a、b的值,并求出{an}的前n项和Sn;
(3)若s>t,且数列{an}是单调递增数列,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com