分析:(1)求出f(x)的导函数,令导函数等于求出x的值,然后由x的值,分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值即可得到f(x)的值域;
(2)设函数g(x)在[0,2]上的值域是A,根据题意对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0,得到区间[0,2]是A的子集,求出g(x)的导函数,分a小于0和a大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于a的不等式,求出不等式的解集即可得到满足题意a的取值范围.
解答:解:(1)对函数f(x)求导,
f′(x)=•.
令f'(x)=0得x=1或x=-1.
当x∈(0,1)时,f'(x)>0,f(x)在(0,1)上单调递增;
当x∈(1,2)时,f'(x)<0,f(x)在(1,2)上单调递减.
又
f(0)=0,f(1)=,f(2)=,
所以当x∈[0,2],f(x)的值域是
[0,];
(2)设函数g(x)在[0,2]上的值域是A.
∵对任意x
1∈[0,2],总存在x
0∈[0,2],使f(x
1)-g(x
0)=0,
∴
[0,]⊆A.
对函数g(x)求导,g'(x)=ax
2-a
2.
①当a<0时,若x∈(0,2),g'(x)<0,所以函数g(x)在(0,2)上单调递减.
∵
g(0)=0,g(2)=a-2a2<0,
∴当x∈[0,2]时,不满足
[0,]⊆A;
②当a>0时,
g′(x)=a(x-)(x+).
令g'(x)=0,得
x=或
x=-(舍去).
(i)当x∈[0,2],
0<<2时,列表:
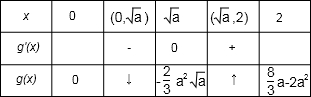
∵
g(0)=0,g()<0,
又∵
[0,]⊆A,∴
g(2)=a-2a2≥,解得
≤a≤1.
(ii)当x∈(0,2),
≥2时,g'(x)<0,∴函数在(0,2)上单调递减,
∵g(0)=0,∴
g(2)=a-2a2<0∴当x∈[0,2]时,不满足
[0,]⊆A.
综上,实数a的取值范围是
[,1].
点评:此题考查学生会利用导函数的正负得到函数的单调区间,会根据函数的增减性得到函数的极值,灵活运用分类讨论的数学思想,会利用导数求函数的值域,是一道综合题.




 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案