
【题目】已知函数f(x)=﹣x2+2x+5,令g(x)=(2﹣2a)x﹣f(x)
(1)若函数g(x)在x∈[0,2]上是单调增函数,求实数a的取值范围;
(2)求函数g(x)在x∈[0,2]的最小值.
【答案】
(1)解:∵f(x)=﹣x2+2x+5,
∴g(x)=(2﹣2a)x﹣f(x)=x2﹣2ax﹣5的图像是开口朝上,且以直线x=a为对称轴的抛物线,
若函数g(x)在x∈[0,2]上是单调增函数,
则a≤0
(2)解:∵g(x)=x2﹣2ax﹣5的图像是开口朝上,且以直线x=a为对称轴的抛物线,
若a<0,则当x=0时,函数g(x)取最小值﹣5,
若0≤a≤2,则当x=a时,函数g(x)取最小值﹣a2﹣5,
若a>2,则当x=2时,函数g(x)取最小值﹣4a﹣15,
综上所述:g(x)min= 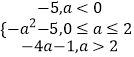
【解析】g(x)=x2﹣2ax﹣5的图像是开口朝上,且以直线x=a为对称轴的抛物线,(1)若函数g(x)在x∈[0,2]上是单调增函数,则a≤0; (2)分类讨论给定区间与对称轴x=a的关系,结合二次函数的图像和性质,可得结论.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


科目:高中数学 来源: 题型:
【题目】若定义在R上的偶函数f(x)在[0,+∞)内是增函数,且f(3)=0,则关于x的不等式xf(x)≤0的解集为( )
A.{x|﹣3≤x≤0或x≥3}
B.{x|x≤﹣3或﹣3≤x≤0}
C.{x|﹣3≤x≤3}
D.{x|x≤﹣3或x≥3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.

(1)求证: ![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成角,如果不存在,请说明理由.
所成角,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+k,且log2f(a)=2,f(log2a)=k,a>0,且a≠1.
(1)求a,k的值;
(2)当x为何值时,f(logax)有最小值?求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校与英国某高中结成友好学校,该校计划选派3人作为交换生到英国进行一个月的生活体验,学校准备从该校英语兴趣小组的6名同学中选派,已知英语兴趣小组中男生有4人,女生有2人
(1)求男生甲或女生乙被选的概率
(2)记选派的3人中的女生人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①若![]() ,则“
,则“![]() ”是“
”是“![]() ”成立的充分不必要条件;
”成立的充分不必要条件;
②若椭圆![]() 的两个焦点为
的两个焦点为![]() ,且弦
,且弦![]() 过点
过点![]() ,则
,则![]() 的周长为16;
的周长为16;
③若命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,则命题
”都是真命题,则命题![]() 一定是真命题;
一定是真命题;
④若命题![]() :
: ![]() ,则
,则![]() :
: ![]()
其中为真命题的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中,正确的是( )
A.2{x|x≤2}
B.3∈{x|x>2且x<1}
C.{x|x=4k±1,k∈Z}≠{x|x=2k+1,k∈Z}
D.{x|x=3k+1,k∈Z}={x|x=3k﹣2,k∈Z}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com