
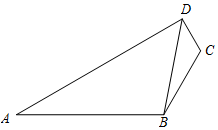
 如图,已知A,B,C,D四点共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC=$\frac{{2\sqrt{7}}}{7}$.
如图,已知A,B,C,D四点共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC=$\frac{{2\sqrt{7}}}{7}$.分析 (Ⅰ)利用已知及同角三角函数基本关系式可求$sin∠BDC=\frac{{\sqrt{21}}}{7}$,进而利用正弦定理即可求得sin∠DBC的值.
(Ⅱ)在△BDC中,由余弦定理可求DB的值,利用同角三角函数基本关系式可求$cos∠DBC=\frac{{5\sqrt{7}}}{14}$,进而利用两角差的余弦函数公式可求cos∠ABD的值,在△ABD中,由余弦定理可求AD的值.
解答 (本小题满分13分)
解:(Ⅰ)在△BDC中,因为$cos∠BDC=\frac{{2\sqrt{7}}}{7}$,
所以$sin∠BDC=\frac{{\sqrt{21}}}{7}$.
由正弦定理$\frac{DC}{sin∠DBC}=\frac{BC}{sin∠BDC}$得,$sin∠DBC=\frac{DC•sin∠BDC}{BC}=\frac{{\sqrt{21}}}{14}$. …(5分)
(Ⅱ)在△BDC中,由BC2=DC2+DB2-2DC•DBcos∠BDC,
得,$4=1+D{B^2}-2DB\frac{{2\sqrt{7}}}{7}$.
所以$D{B^2}-\frac{{4\sqrt{7}}}{7}DB-3=0$.
解得$DB=\sqrt{7}$或$DB=-\frac{{3\sqrt{7}}}{7}$(舍).
由已知得∠DBC是锐角,又$sin∠DBC=\frac{{\sqrt{21}}}{14}$,
所以$cos∠DBC=\frac{{5\sqrt{7}}}{14}$.
所以cos∠ABD=cos(120°-∠DBC)=cos120°•cos∠DBC+sin120°•sin∠DBC=$-\frac{1}{2}•\frac{{5\sqrt{7}}}{14}+\frac{{\sqrt{3}}}{2}•\frac{{\sqrt{21}}}{14}$=$-\frac{{\sqrt{7}}}{14}$.
在△ABD中,因为AD2=AB2+BD2-2AB•BDcos∠ABD=$16+7-2×4×\sqrt{7}×(-\frac{{\sqrt{7}}}{14})=27$,
所以$AD=3\sqrt{3}$. …(13分)
点评 本题主要考查了同角三角函数基本关系式,正弦定理,余弦定理,两角差的余弦函数公式在解三角形中的综合应用,考查了计算能力和转化思想,数形结合思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=\sqrt{3},b=1$ | |
| B. | 不等式f(x1)f(x2)≤4取到等号时|x1-x2|的最小值为2π | |
| C. | 函数f(x)的图象一个对称中心为 $({\frac{2}{3}π,0})$ | |
| D. | 函数f(x)在区间$[{\frac{π}{6},π}]$上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?β,m⊥n,则α⊥β | B. | 若α∥β,m⊥α,n∥β,则 m⊥n | ||
| C. | 若α⊥β,m⊥α,n∥β,则m∥n | D. | 若α⊥β,α∩β=m,n⊥m,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M∩N={3} | C. | M∪N={0} | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,α∥β,则m∥β | C. | 若m?α,m⊥β,则α⊥β | D. | 若m?α,α⊥β,则m⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某农户计划建造一个室内面积为800m2的矩形蔬菜温室,在温室外,沿左、右两侧与后侧各保留1m宽的通道,沿前侧保留3m的空地(如图所示),当矩形温室的长和宽分别为多少时,总占地面积最大?并求出最大值.
某农户计划建造一个室内面积为800m2的矩形蔬菜温室,在温室外,沿左、右两侧与后侧各保留1m宽的通道,沿前侧保留3m的空地(如图所示),当矩形温室的长和宽分别为多少时,总占地面积最大?并求出最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com