
 某农户计划建造一个室内面积为800m2的矩形蔬菜温室,在温室外,沿左、右两侧与后侧各保留1m宽的通道,沿前侧保留3m的空地(如图所示),当矩形温室的长和宽分别为多少时,总占地面积最大?并求出最大值.
某农户计划建造一个室内面积为800m2的矩形蔬菜温室,在温室外,沿左、右两侧与后侧各保留1m宽的通道,沿前侧保留3m的空地(如图所示),当矩形温室的长和宽分别为多少时,总占地面积最大?并求出最大值. 分析 设出矩形的长为a与宽b,建立蔬菜面积关于矩形边长的函数关系式S=(a-4)(b-2)=ab-4b-2a+8=800-2(a+2b).利用基本不等式变形求解.
解答 解:设矩形温室的左侧边长为am,后侧边长为bm,则ab=800.
蔬菜的种植面积
S=(a-4)(b-2)
=ab-4b-2a+8
=808-2(a+2b).
所以S≤808-4$\sqrt{2ab}$=648(m2),当且仅当a=2b,即a=40(m),b=20(m)时,S最大值=648(m2).
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648m2.
点评 本题考查函数的模型的选择与应用,基本不等式的应用,基本知识的考查.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
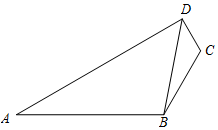 如图,已知A,B,C,D四点共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC=$\frac{{2\sqrt{7}}}{7}$.
如图,已知A,B,C,D四点共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC=$\frac{{2\sqrt{7}}}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|;
已知函数f(x)=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|;| 性质 | 定义域 | 值域 | 单调性 | 奇偶性 | 零点 |
| f(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com