Question

16．已知函数f（x）=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|；
（1）作出函数f（x）的图象；
（2）根据（1）所得图象，填写下面的表格：

性质	定义域	值域	单调性	奇偶性	零点
f（x）

（3）关于x的方程f²（x）+m|f（x）|+n=0（m，n∈R）恰有6个不同的实数解，求n的取值范围．

Answer 1

分析 （1）利用分段函数求出f（x）的表达式，然后作出函数f（x）的图象，
（2）结合函数的图象判断相应的性质，
（3）根据图象利用换元法将条件进行转化，利用数形结合即可得到结论．

解答 解：函数f（x）=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|=$\left\{\begin{array}{l}{\frac{2}{x}，}&{x≥1}\\{2x，}&{0＜x＜1}\\{-2x，}&{-1≤x＜0}\\{-\frac{2}{x}，}&{x＜-1}\end{array}\right.$，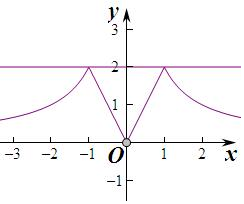
作出函数f（x）的图象如图：
（2）由函数的图象得函数的定义域为{x|x≠0}，
函数的值域为（0，2]，
在（-∞，-1]和（0，1）上单调递增，
在[1，+∞）和（-1，0），单调递减，
函数关于y轴对称，是偶函数，
函数与x轴没有交点，无零点．
（3）∵0＜f（x）≤2，且函数f（x）为偶函数，
∴令t=f（x），则方程等价为t²+mt+n=0，
则由图象可知，当0＜t＜2时，方程t=f（x）有4个不同的根，
当t=2时，方程t=f（x）有2个不同的根，
当t≤0或t＞2时，方程t=f（x）有0个不同的根，
若方程f²（x）+m|f（x）|+n=0（m，n∈R）恰有6个不同的实数解，等价为方程f²（x）+mf（x）+n=0（m，n∈R）恰有6个不同的实数解，
即t²+mt+n=0有两个不同的根，
其中t₁=2，0＜t₂＜2，
则n=t₁t₂∈（0，4）．

点评 本题主要考查函数零点的应用，利用条件求出函数f（x）的表达式，利用数形结合是解决本题的关键，综合性较强，难度较大．