
分析 (1)求出f(x)的导数,令导数大于0,得增区间,令导数小于0,得减区间,进而求得f(x)的值域;
(2)对于任意x0∈[0,1],总存在x1,x2∈($\frac{1}{e}$,e3),x1≠x2,使得g(x1)=g(x2)=f(x0)成立,即函数g(x)在区间($\frac{1}{e}$,e3)上不是单调函数.…构造函数g(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,x∈($\frac{1}{e}$,e3),再由导数求得g(x)的最值,即可得到所求范围.
解答 解:(1)f′(x)=$\frac{-(2x-1)(2x-7)}{(2-x)^{2}}$,x∈[0,1].…(2分)
f′(x)>0,解得$\frac{1}{2}$<x<1,
f′(x)<0,解得0<x<$\frac{1}{2}$,
所以函数f(x)在($\frac{1}{2}$,1)上是增函数,在(0,$\frac{1}{2}$)上是减函数.…(4分)
f($\frac{1}{2}$)=-4,f(0)=-$\frac{7}{2}$,f(1)=-3.
所以函数f(x)的单调增区间为($\frac{1}{2}$,1),单调减区间为(0,$\frac{1}{2}$),值域为[-4,-3].…(6分)
(2)因为对于任意x0∈[0,1],总存在x1,x2∈($\frac{1}{e}$,e3),x1≠x2,使得g(x1)=g(x2)=f(x0)成立,
所以函数g(x)在区间($\frac{1}{e}$,e3)上不是单调函数.…(8分)
g(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,x∈($\frac{1}{e}$,e3).
因为g(x)在区间($\frac{1}{e}$,e3)上不是单调函数,所以$\frac{1}{e}$<x≤a,①且易知g(x)在区间($\frac{1}{e}$,a)上是减函数,在区间(a,e3)上是增函数.…(10分)
当$\frac{1}{e}$<x≤a时,g(a)≤g(x)<$\frac{1}{e}$-4+a;当a≤x<e<3<时,g(a)≤g(x)<e3-4-3a.
根据题意,得g(a)<-4,②$\frac{1}{e}$-4+a>-3,③e3-4-3a>-3.④…(14分)
解由①②③④组成的不等式组,得e<x<$\frac{{e}^{3}-1}{3}$.
所以a的取值范围为(e,$\frac{{e}^{3}-1}{3}$)…(16分)
点评 本题考查导数的运用:求单调区间和极值,主要考查不等式恒成立和存在性问题,注意运用参数分离和构造函数通过导数判断单调性,求出最值,属于难题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | α⊥β,l∥α⇒l⊥β | B. | α⊥β,l⊥α⇒l∥β | C. | α∥β,l∥α⇒l∥β | D. | α∥β,l⊥α⇒l⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值是1,最小值是$-\sqrt{3}$ | B. | 最大值是1,最小值是-1 | ||
| C. | 最大值是2,最小值是$-\sqrt{3}$ | D. | 最大值是2,最小值是-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
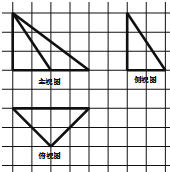 如图是某四面体ABCD水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD外接球的表面积为( )
如图是某四面体ABCD水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD外接球的表面积为( )| A. | 20π | B. | $\frac{125}{6}π$ | C. | 25π | D. | 100π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com