
分析 ①由题意可得:$\left\{\begin{array}{l}{△=(a-3)^{2}-4a>0}\\{a<0}\end{array}\right.$,解出a,即可判断出结论;
②x=0时,f(0)=0,即可判断出正误;
③变形:函数$y=\frac{{3-{2^x}}}{{{2^x}+2}}$=$\frac{5-(2+{2}^{x})}{2+{2}^{x}}$=$\frac{5}{2+{2}^{x}}$-1,由2x>0,可得$\frac{1}{2+{2}^{x}}$∈$(0,\frac{1}{2})$,进而得出值域.
④不妨设正四面体 A-BCD的棱长为2,内切球的半径为r,外接球的半径为R,利用三棱锥体积计算公式可得:解得r,R.即可判断出结论.
解答 解:①方程x2+(a-3)x+a=0有一个正实根,一个负实根,∴$\left\{\begin{array}{l}{△=(a-3)^{2}-4a>0}\\{a<0}\end{array}\right.$,解得a<0,故①正确;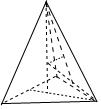
②f(x)是定义在R上的奇函数,当x<0时,f(x)=2x2+x-1,则x=0时,f(0)=0;
x>0时,-x<0,f(-x)=2x2-x-1,则f(x)=-f(-x)=-2x2+x+1,故②不正确.
③函数$y=\frac{{3-{2^x}}}{{{2^x}+2}}$=$\frac{5-(2+{2}^{x})}{2+{2}^{x}}$=$\frac{5}{2+{2}^{x}}$-1,∵2x>0,∴$\frac{1}{2+{2}^{x}}$∈$(0,\frac{1}{2})$,∴y∈$({-1,\frac{3}{2}})$,故③正确.
④不妨设正四面体 A-BCD的棱长为2,内切球的半径为r,外接球的半径为R,则$\frac{1}{3}×$$\frac{\sqrt{3}}{4}$×22•r×4=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{2}^{2}$×$\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}$,$(\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}-R)^{2}$+$(\frac{2\sqrt{3}}{3})^{2}$=R2,解得r=$\frac{1}{\sqrt{6}}$,R=$\frac{3}{\sqrt{6}}$.则$\frac{{V}_{1}}{{V}_{2}}$=$(\frac{r}{R})^{3}$=$\frac{1}{27}$,
故④正确.
故答案为:①③④.
点评 本题考查了函数的奇偶性单调性、一元二次方程的方程的实数根与判别式的关系、正四面体与正三角形的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
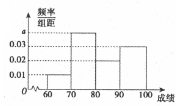 在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{4}{25}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com