
| A. | $\frac{4}{9}$ | B. | $\frac{4}{25}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
分析 根据题意得到△DEF∽△ABC,则相似三角形的面积之比等于相似比的平方.
解答 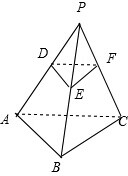 解:如图,∵平面DEF∥平面ABC,
解:如图,∵平面DEF∥平面ABC,
∴△DEF∽△ABC,DE∥AB,EF∥BC,DF∥AC,
∴$\frac{DE}{AB}$=$\frac{PD}{PA}$.
又$\frac{PD}{DA}$=$\frac{PE}{EB}$=$\frac{PF}{FC}$=$\frac{2}{3}$,
∴$\frac{PD}{PA}$=$\frac{2}{5}$,
∴$\frac{DE}{AB}$=$\frac{PD}{PA}$=$\frac{2}{5}$,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{2}{5}$)2=$\frac{4}{25}$.
故选:B.
点评 本题考查了平面与平面平行的性质:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 0 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com