练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，底面是平行四边形的四棱锥P-ABCD，M是PD的中点，N是MD的中点，PE：EC=2：1，求证：
    （1）PB∥面MAC；
    （2）BE∥面ANC．
    考点：直线与平面平行的判定
    专题：空间位置关系与距离
    分析：根据线面平行的判定定理分别进行判断即可．
    解答： 证明：（1）连BD交AC于O，连MO，
    ∵M是PD的中点，O是BD的中点，
    ∴PB∥MO，
    ∵MO?面AMC，
    ∴PB∥面MAC；
    （2）连ME、BM，连BD交AC于O，连NO，
    ∵PC：EC=PM：AM=2：1
    ∴ME∥NC，∴ME∥面ANC
    ∵N为MD的中点，∴NO∥BM，∴BM∥面ANC，
    即
    ME/面/ANC
    BM∥面ANC
    ME∩BM=M
    ⇒面BME∥面ANC
    ∵BE?面BME，
    ∴BE∥面ANC
    点评：本题主要考查线面平行的判定，根据线面平行的判定定理或面面平行的性质定理是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=ex的图象与g（x）的图象关于直线y=x对称．
    （1）若直线y=kx+1与g（x）的图象相切，求实数k的值；
    （2）判断曲线y=f（x）与曲线y=
    1
    2
    x2+ax+1（a∈R）公共点的个数；
    （3）设a＜b，比较f（
    a+b
    2
    ）与
    f(b)-f(a)
    b-a
    的大小，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列an=n2sin
    nπ
    2
    ，则a1+a2+a3+…+a100=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知F（X）是奇函数，且有f（x+1）=-
    1
    f(x)
    ，当x∈（0，
    1
    2
    ）时，f（x）=8x．
    （1）求f（-
    1
    3
    ），f（
    2
    3
    ），f（
    5
    3
    ）的值；
    （2）当2k+
    1
    2
    ＜x＜2k+1，（k∈Z）时，求f（x）的解析式；
    （3）是否存在k∈N*，使2k+
    1
    2
    ＜x＜2k+1时，不等式log8f（x）＞x2-（k+3）x-k+2有解？若存在，求出k的值及对应的不等式的解；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

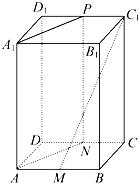    如图，长方体ABCD-A1B1C1D1中，M，N，P分别为线段AB，CD，C1D1的中点．求证：
    （1）C1M∥平面ANPA1；
    （2）平面C1MC∥平面ANPA1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    抛物线y=2ax2的准线方程是y=2，则a的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知两条直线l1：y=m和l2：y=
    8
    2m+1
    （m＞0），l1与函数y=|log2x|的图象从左至右相交于点A、B，l2与函数y=|log2x|的图象从左至右相交于点C、D．记线段AC和BD在x轴上的投影长度分别为a、b．当m变化时，求
    b
    a
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

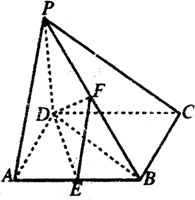    如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC=2，E、F分别是PB，AB的中点．
    （1）求证：CD∥面PAB；
    （2）求证：EF⊥CD；
    （3）求三棱锥B-DEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    随着社会的发展，网上购物已成为一种新型的购物方式．某商家在网上新推出A，B，C，D四款商品，进行限时促销活动，规定每位注册会员限购一件，并需在网上完成对所购商品的质量评价．以下为四款商品销售情况的条形图和用分层抽样法选取100份评价的统计表：
     好评中评差评
    款80%15%5%
    款88%12%0
    款80%10%10%
    款84%8%8%
    （1）若会员甲选择的是A款商品，求甲的评价被选中的概率；
    （2）在被选取的100份评价中，若商家再选取2位评价为差评的会员进行电话回访，求这2位中至少有一位购买的是C款商品的概率．

    查看答案和解析>>

    同步练习册答案