
 件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把
件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把 件打成一包,对这
件打成一包,对这 件产品进行一次性整体检验,如
件产品进行一次性整体检验,如 果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了
果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了 次
次 测这
测这 件产品的检测次数
件产品的检测次数 ;
; ,要使检测次数最少,则每包应放多少件产品?
,要使检测次数最少,则每包应放多少件产品? 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
 度的人数如下表:
度的人数如下表:| 喜爱程度 | 喜欢 | 一般 | 不喜欢 |
| 人数 | 560 | 240 | 200 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,众数为
,众数为 ,平均值为
,平均值为 ,则( )
,则( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.为60.316 kg | B.约为60.316 kg |
| C.大于60.316 kg | D.小于60.316 kg |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 课本上抄录一个随机变量
课本上抄录一个随机变量
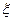 的概率分布列如下表:
的概率分布列如下表:
 同学计算
同学计算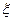 的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同.据此,小王给出了正确答案
的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同.据此,小王给出了正确答案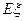 = .
= .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
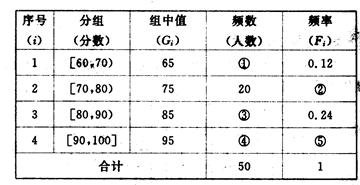
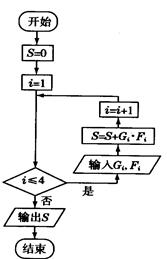
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 区人均消费y进行统计调查得y与x具有相关关系,且回归直线方程为
区人均消费y进行统计调查得y与x具有相关关系,且回归直线方程为 (单位:千
(单位:千 元),若该地区人均消费水平为7.675,估计该地区人均消费额占人均工资收入的百分比约为____________。
元),若该地区人均消费水平为7.675,估计该地区人均消费额占人均工资收入的百分比约为____________。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com