
| A. | 6 | B. | 5 | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
分析 由$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{6-m}$=1是焦点在x轴上的椭圆,可得m>6-m>0,求出m的范围,再由直线y=kx+1恒过定点,且与椭圆恒有公共点,进一步求得m的范围得答案.
解答 解:∵$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{6-m}$=1是焦点在x轴上的椭圆,
∴m>6-m>0,即3<m<6,
又直线y=kx+1恒过定点(0,1),
且椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{6-m}$=1与y=kx+1恒有公共点,
则6-m≤1,即m≥5,
综上,5≤m<6.
故选:B.
点评 本题考查椭圆的简单性质,考查了直线恒过定点问题,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
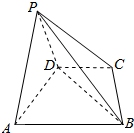 在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com