
���� ��1����x��y��ʾ������t���г������������ɣ�
��2���������C����ͨ���̣����ô����������AB����AB���ϸߵ����ֵ��
��� �⣺��1����x=cos90��+tcos60��=$\frac{1}{2}t$��t=2x����y=cos45��+tcos30��=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$t��t=$\frac{2\sqrt{3}}{3}$y-$\frac{\sqrt{6}}{3}$��
��ֱ��l��ֱ�����귽��Ϊ2x=$\frac{2\sqrt{3}}{3}$y-$\frac{\sqrt{6}}{3}$����6x-2$\sqrt{3}$y+$\sqrt{6}$=0������б��ʽ����Ϊy=$\sqrt{3}$x+$\frac{\sqrt{2}}{2}$��
ֱ��l��б��Ϊ$\sqrt{3}$����ֱ��l����б��Ϊ60�㣮
��2��������C�����귽��Ϊ����=-2cos����+$\frac{3��}{4}$��=$\sqrt{2}$cos��+$\sqrt{2}$sin�ȣ����2=$\sqrt{2}��$cos��+$\sqrt{2}$��sin�ȣ�
������C��ֱ�����귽��Ϊx2+y2=$\sqrt{2}$x+$\sqrt{2}$y������x-$\frac{\sqrt{2}}{2}$��2+��y-$\frac{\sqrt{2}}{2}$��2=1��
������C��ʾ�ԣ�$\frac{\sqrt{2}}{2}$��$\frac{\sqrt{2}}{2}$��ΪԲ�ģ���r=1Ϊ�뾶��Բ��
Բ�ĵ�ֱ��l�ľ���d=$\frac{3\sqrt{2}}{\sqrt{36+12}}$=$\frac{\sqrt{6}}{4}$����AB=2$\sqrt{{r}^{2}-{d}^{2}}$=$\frac{\sqrt{10}}{2}$��
���ABC��������ֵΪ$\frac{1}{2}$AB����d+r��=$\frac{1}{2}��\frac{\sqrt{10}}{2}����1+\frac{\sqrt{6}}{4}��$=$\frac{2\sqrt{10}+\sqrt{15}}{8}$��
���� ���⿼���˲������̣������귽����ֱ�����귽�̵�ת����ֱ������Բ��λ�ù�ϵ�������е��⣮


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
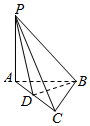 ������P-ABCD�У�����ABCΪֱ�������Σ�AB=BC��PA��ƽ��ABC��
������P-ABCD�У�����ABCΪֱ�������Σ�AB=BC��PA��ƽ��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{7}}}{7}$ | B�� | $\frac{{2\sqrt{7}}}{7}$ | C�� | $\frac{{\sqrt{21}}}{7}$ | D�� | $\frac{{2\sqrt{21}}}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
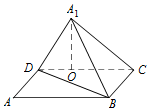 ��ͼ����֪����ABCD�У�AB=10��BC=6���������ضԽ���BD�ѡ�ABD����ʹA�Ƶ�A1�㣬��A1��ƽ��BCD�ϵ���ӰOǡ��CD�ϣ���A1O��ƽ��DBC��
��ͼ����֪����ABCD�У�AB=10��BC=6���������ضԽ���BD�ѡ�ABD����ʹA�Ƶ�A1�㣬��A1��ƽ��BCD�ϵ���ӰOǡ��CD�ϣ���A1O��ƽ��DBC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 5 | C�� | $\frac{5}{3}$ | D�� | -$\frac{5}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ƽ��ֱ������ϵxOy�У���Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����ΪA��-3��0����Բ����ԭ���ԲO����Բ���ڽ������Ρ�AEF�������߶����У�
��֪��ƽ��ֱ������ϵxOy�У���Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����ΪA��-3��0����Բ����ԭ���ԲO����Բ���ڽ������Ρ�AEF�������߶����У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
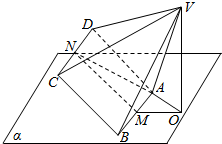 ��ͼ������Ϊ�������Ҹ����ⳤ����ȵ�����V-ABCD��������AB������ת����AB?ƽ�����M��N�ֱ���AB��CD���е㣬AB=2��VA=$\sqrt{5}$����V��ƽ����ϵ���ӰΪ��O����ON�����ʱ�������C-AB-O�Ĵ�С�ǣ�������
��ͼ������Ϊ�������Ҹ����ⳤ����ȵ�����V-ABCD��������AB������ת����AB?ƽ�����M��N�ֱ���AB��CD���е㣬AB=2��VA=$\sqrt{5}$����V��ƽ����ϵ���ӰΪ��O����ON�����ʱ�������C-AB-O�Ĵ�С�ǣ�������| A�� | 90�� | B�� | 105�� | C�� | 120�� | D�� | 135�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com