
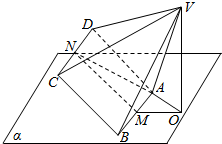
 如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )
如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )| A. | 90° | B. | 105° | C. | 120° | D. | 135° |
分析 根据条件确定二面角的平面角,结合余弦定理以及两角和差的余弦公式以及倍角公式进行求解即可.
解答 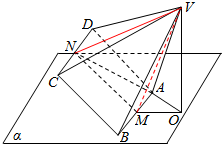 解:设∠VMO=θ,
解:设∠VMO=θ,
则∵M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,
∴AM=1,VM=$\sqrt{V{A}^{2}-A{M}^{2}}$=$\sqrt{5-1}=\sqrt{4}$=2,
MN=BC=AB=2,VN=VM=2,
则三角形VNM为正三角形,则∠NMV=60°,
则OM=2cosθ,
在三角形OMN中,
ON2=MN2+OM2-2MN•OMcos(60°+θ)=4+4cos2θ-2×2×2cosθcos(60°+θ)
=4+4cos2θ-8cosθ($\frac{1}{2}$cosθ-$\frac{\sqrt{3}}{2}$sinθ)
=4+4cos2θ-4cos2θ+4$\sqrt{3}$sinθcosθ
=4+2$\sqrt{3}$sin2θ,
∴要使ON最大,则只需要sin2θ=1,即2θ=90°即可,则θ=45°,
此时二面角C-AB-O的大小∠OMN=60°+θ=60°+45°=105°,
故选:B
点评 本题主要考查二面角的求解,根据条件求出二面角的平面角.结合余弦定理以及两角和差的余弦公式进行化简是解决本题的关键.


科目:高中数学 来源: 题型:解答题
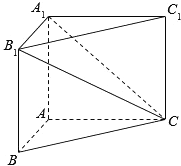 直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4.
直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com