
分析 (1)根据条件,奇函数f(x)在原点有定义,从而f(0)=b=0,从而$f(x)=\frac{\sqrt{a}x}{1+{x}^{2}}$,而根据$f(\frac{1}{2})=\frac{2}{5}$便可求出a=1,这样便得出a,b的值;
(2)写出$f(x)=\frac{x}{1+{x}^{2}}$,根据单调性的定义,设任意的x1,x2∈(-1,1),且x1<x2,然后作差,通分,提取公因式,便得到$f({x}_{1})-f({x}_{2})=\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{(1+{{x}_{1}}^{2})(1+{{x}_{2}}^{2})}$,可以说明f(x1)<f(x2),从而得出f(x)在(-1,1)上为增函数.
解答 解:(1)∵f(x)是定义在(-1,1)上的奇函数;
∴f(0)=b=0;
得$f(x)=\frac{{\sqrt{a}x}}{{1+{x^2}}}$;
而$f(\frac{1}{2})=\frac{2}{5}\sqrt{a}=\frac{2}{5}$;
∴a=1;
∴a=1,b=0;
(2)$f(x)=\frac{x}{1+{x}^{2}}$,设x1,x2∈(-1,1)且x1<x2,则:
$f({x_1})-f({x_2})=\frac{{({x_1}-{x_2})(1-{x_1}{x_2})}}{{({x_1}^2+1)({x_2}^2+1)}}$;
∵x1,x2∈(-1,1),且x1<x2;
∴x1-x2<0,x1x2<1,1-x1x2>0;
∴$\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{({{x}_{1}}^{2}+1)({{x}_{2}}^{2}+1)}<0$;
∴f(x1)<f(x2);
∴f(x)在(-1,1)上为增函数.
点评 考查奇函数的定义,奇函数在原点有定义时,原点处的函数值为0,以及函数单调性的定义,根据单调性定义判断一个函数单调性的方法和过程,作差的方法比较f(x1),f(x2),作差后,是分式的一般要通分,一般要提取公因式x1-x2.


科目:高中数学 来源: 题型:选择题
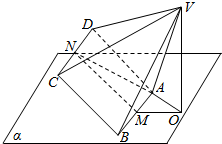 如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )
如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )| A. | 90° | B. | 105° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{6}}}{9}$ | D. | $\frac{{5\sqrt{3}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{10}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com