
分析 (1)运用椭圆的离心率公式和点满足椭圆方程,解方程可得a,b,进而得到椭圆方程;
(2)分类讨论:当AB或CD中的一条与x轴垂直而另一条与x轴重合时,此时四边形ABCD面积S=2b2.当直线AC和BD的斜率都存在时,不妨设直线AC的方程为y=k(x-1),则直线BD的方程为y=-$\frac{1}{k}$(x-1).分别与椭圆的方程联立得到根与系数的关系,利用弦长公式可得|AB|,|CD|.利用四边形ABCD面积S=$\frac{1}{2}$|AB|•|CD|,即可得到关于斜率k的式子,再利用配方和二次函数的最值求法,即可得出.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{1}{2}$,a2-b2=c2,
$\frac{3}{{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,
解得a=2,b=$\sqrt{3}$,
即有椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1可得a2=4,b2=3,c=$\sqrt{{a}^{2}-{b}^{2}}$=1.
①当AB或CD中的一条与x轴垂直而另一条与x轴重合时,
此时四边形ACBD面积S=$\frac{1}{2}$•2a•$\frac{2{b}^{2}}{a}$=2b2=6.
②当直线AB和CD的斜率都存在时,不妨设直线AB的方程为y=k(x-1),
则直线CD的方程为y=-$\frac{1}{k}$(x-1).
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,化为(3+4k2)x2-8k2x+4k2-12=0,
∴x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$.
∴|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$
=$\sqrt{(1+{k}^{2})[(\frac{8{k}^{2}}{3+4{k}^{2}})^{2}-\frac{16{k}^{2}-48}{3+4{k}^{2}}]}$=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$.
把k换成-$\frac{1}{k}$,可得|CD|=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$.
∴四边形ACBD面积S=$\frac{1}{2}$|AB|•|CD|=$\frac{1}{2}$•$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$•$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$
=$\frac{1}{2}$•$\frac{144(1+{k}^{2})^{2}}{12{k}^{4}+25{k}^{2}+12}$=$\frac{1}{2}$•$\frac{144}{-(\frac{1}{1+{k}^{2}}-\frac{1}{2})^{2}+\frac{49}{4}}$,
当且仅当$\frac{1}{1+{k}^{2}}$=$\frac{1}{2}$,即k2=1时,S取得最小值$\frac{288}{49}$.
综上可知:四边形ACBD的面积S的最小值是$\frac{288}{49}$.
点评 本题考查椭圆的标准方程及其性质、相互垂直的直线斜率之间的关系、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、四边形面积计算公式、二次函数的最值求法等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
 如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
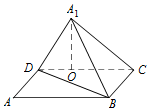 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.
已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
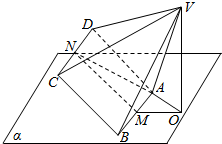 如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )
如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )| A. | 90° | B. | 105° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{6}}}{9}$ | D. | $\frac{{5\sqrt{3}}}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com