
分析 先计算投入带来的销售额增加值,再利用导数法,即可确定函数的最值.
解答 解:设3百万元中技术改造投入为x(百万元),广告费投入为3-x(百万元),…(1分)
则广告收入带来的销售额增加值为-2(3-x)2+14(3-x)(百万元),
技术改造投入带来的销售额增加值为-$\frac{1}{3}$x3+2x2+5x(百万元),…(3分)
所以,投入带来的收益F(x)=-2(3-x)2+14(3-x)-$\frac{1}{3}$x3+2x2+5x-3.
整理上式得F(x)=-$\frac{1}{3}$x3+3x+21,…(6分)
因为F′(x)=-x2+3,
令F′(x)=0,解得x=$\sqrt{3}$或x=-$\sqrt{3}$(舍去),
当x∈[0,$\sqrt{3}$),F′(x)>0,当x∈($\sqrt{3}$,3]时,F′(x)<0,…(10分)
所以,x=$\sqrt{3}$≈1.73时,F(x)取得最大值.…(11分)
所以,当该公司用于广告投入1.27(百万元),用于技术改造投入1.73(百万元)时,公司将获得最大收益.…(12分)
点评 本题考查函数模型的构建,考查导数知识的运用,考查学生的计算能力,正确确定函数解析式是关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
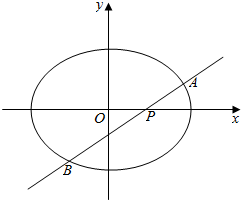 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
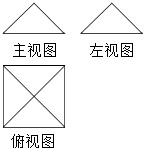 一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )
一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )| A. | 48 | B. | 64 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{6}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com