
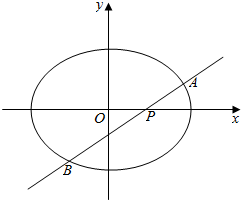
 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.分析 (1)由椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,利用椭圆简单性质列出方程组,求出a,b,由此能求出椭圆E的方程.
(2)设A(x1,y1),B(x2,y2),则$\frac{{{x_1}^2}}{2}+{y_1}^2=1,\frac{{{x_2}^2}}{2}+{y_2}^2=1$,由此利用点差法能证明k1+k2=0.
(3)当直线l与y轴平行时,Q点的坐标为(x0,0);当直线l与y轴垂直时,Q点坐标只可能为$(\frac{2}{t},0)$,再证明对任意直线l,均有$\frac{QA}{QB}=\frac{PA}{PB}$即可.
解答 解:(1)∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,
∴$\left\{\begin{array}{l}\frac{1}{a^2}+\frac{1}{{2{b^2}}}=1\\{a^2}-{b^2}={c^2}\\ \frac{c}{a}=\frac{{\sqrt{2}}}{2}\end{array}\right.$,解得a=2,b=1.
∴椭圆E的方程为$\frac{x^2}{2}+{y^2}=1$.(4分)
证明:(2)设A(x1,y1),B(x2,y2),则$\frac{{{x_1}^2}}{2}+{y_1}^2=1,\frac{{{x_2}^2}}{2}+{y_2}^2=1$.
由题意P(1,0),Q(2,0),
∵$\overrightarrow{AP}∥\overrightarrow{BP}∴({{x_1}-1,{y_1}})∥({{x_2}-1,{y_2}})∴{x_1}{y_2}-{x_2}{y_1}={y_1}-{y_2}$.
$\begin{array}{l}∵({{x_1}{y_2}-{x_2}{y_1}})({{x_1}{y_2}+{x_2}{y_1}})={x_1}^2{y_2}^2-{x_2}^2{y_1}^2=({2-{y_1}^2}){y_2}^2-({2-{y_2}^2}){y_1}^2\\=2{y_2}^2-2{y_1}^2\end{array}$
∴$({{x_1}{y_2}+{x_2}{y_1}})({{y_1}-{y_2}})=2{y_2}^2-2{y_1}^2=2({{y_1}-{y_2}})({{y_1}+{y_2}})$,
若y1=y2,则k1=k2=0,结论成立.(此处不交代扣1分)
若y1≠y2,则x1y2+x2y1=2(y1+y2),
∴${k_1}+{k_2}=\frac{y_1}{{{x_1}-2}}+\frac{y_2}{{{x_2}-2}}=\frac{{{x_1}{y_2}+{x_2}{y_1}-2({{y_1}+{y_2}})}}{{({{x_1}-2})({{x_2}-2})}}=0$.(10分)
备注:本题用相似三角形有关知识证明同样给分,用韦达定理解决也相应给分.
解:(3)当直线l与y轴平行时,设直线l与椭圆相交于C,D两点,
如果存在定点Q满足条件,则有$\frac{QC}{QD}=\frac{PC}{PD}$,即QC=QD,
∴Q在x轴上,可设Q点的坐标为(x0,0).
当直线l与y轴垂直时,设直线$\frac{π}{3}$与椭圆相交于M,N两点,则M,N的坐标分别为$(\sqrt{2},0),(-\sqrt{2},0)$,
由$\frac{QM}{QN}=\frac{PM}{PN}$,有$|{\frac{{{x_0}-\sqrt{2}}}{{{x_0}+\sqrt{2}}}}|=|{\frac{{\sqrt{2}-t}}{{\sqrt{2}+t}}}|$,解得${x_0}=\frac{2}{t}$.
∴若存在不同于点P不同的定点Q满足条件,则Q点坐标只可能为$(\frac{2}{t},0)$.(12分)
下面证明:对任意直线l,均有$\frac{QA}{QB}=\frac{PA}{PB}$.
记直线AQ的斜率为k1,直线BQ的斜率为k2,
设A(x1,y1),B(x2,y2),则$\frac{{{x_1}^2}}{2}+{y_1}^2=1,\frac{{{x_2}^2}}{2}+{y_2}^2=1$.
由题意$P({t,0}),Q({\frac{2}{t},0})$,
∵$\overrightarrow{AP}∥\overrightarrow{BP}∴({{x_1}-t,{y_1}})∥({{x_2}-t,{y_2}})∴{x_1}{y_2}-{x_2}{y_1}=t({{y_1}-{y_2}})$.
$\begin{array}{l}∵({{x_1}{y_2}-{x_2}{y_1}})({{x_1}{y_2}+{x_2}{y_1}})={x_1}^2{y_2}^2-{x_2}^2{y_1}^2=({2-{y_1}^2}){y_2}^2-({2-{y_2}^2}){y_1}^2\\=2{y_2}^2-2{y_1}^2\end{array}$
∴$({{x_1}{y_2}+{x_2}{y_1}})t({{y_1}-{y_2}})=2{y_2}^2-2{y_1}^2=2({{y_1}-{y_2}})({{y_1}+{y_2}})$
若y1=y2,则k1=k2=0.
$若{y_1}≠{y_2}则{x_1}{y_2}+{x_2}{y_1}=\frac{2}{t}({{y_1}+{y_2}})$∴${k_1}+{k_2}=\frac{y_1}{{{x_1}-\frac{2}{t}}}+\frac{y_2}{{{x_2}-\frac{2}{t}}}=\frac{{{x_1}{y_2}+{x_2}{y_1}-\frac{2}{t}({{y_1}+{y_2}})}}{{({{x_1}-\frac{2}{t}})({{x_2}-\frac{2}{t}})}}=0$.
点B于x轴对称的点B'的坐标为(-x2,y2).∴kQA=kQB′,∴Q,A,B'三点共线.
∴$\frac{QA}{QB}=\frac{QA}{QB'}=\frac{{|{y_1}|}}{{|{y_2}|}}=\frac{PA}{PB}$.∴对任意直线l,均有$\frac{QA}{QB}=\frac{PA}{PB}$.(16分)
点评 本题考查椭圆方程的求法,考查k1+k2=0的证明,考查是否存在与点P不同的定点Q,使得$\frac{QA}{QB}$=$\frac{PA}{PB}$恒成立的判断与证明,是中档题,解题时要认真审题,注意椭圆性质、椭圆与直线位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{4028}{2015}$ | D. | $\frac{2014}{4030}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
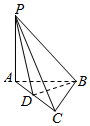 在三棱锥P-ABCD中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.
在三棱锥P-ABCD中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{2\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{7}$ | D. | $\frac{{2\sqrt{21}}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
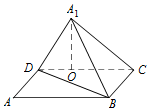 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.
已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com