
| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{2\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{7}$ | D. | $\frac{{2\sqrt{21}}}{7}$ |
分析 设球O的半径为R,当∠AOC=∠BOC=90°时,△AOC和△BOC的面积之和最大,由此能求出O到面ABC的距离.
解答 解:设球O的半径为R,
∵S△AOC+S△BOC=$\frac{1}{2}{R}^{2}$(sin∠AOC+sin∠BOC),-
∴当∠AOC=∠BOC=90°时,△AOC和△BOC的面积之和最大,
此时OA⊥OC,OB⊥OC,
∴OC⊥平面AOB,
∴VO-ABC=VC-OAB=$\frac{1}{3}OC×\frac{1}{2}OA•OBsin∠AOB$=$\frac{1}{6}{R}^{3}sin60°$=$\frac{2\sqrt{3}}{3}$,
∵AC=BC=$\sqrt{4+4}=2\sqrt{2}$,AB=2,∴${S}_{△ABC}=\frac{1}{2}×2×\sqrt{(2\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{7}$,
设O到面ABC的距离为h,则VO-ABC=$\frac{1}{3}×{S}_{△ABC}×h=\frac{2\sqrt{3}}{3}$,
解得h=$\frac{2\sqrt{21}}{7}$.
∴O到面ABC的距离为$\frac{2\sqrt{21}}{7}$.
故选:D.
点评 本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意等体积法的合理运用.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
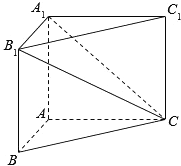 直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4.
直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
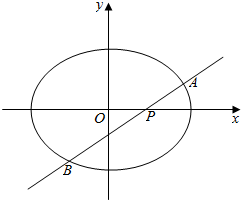 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com