
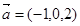 ,
,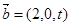 且
且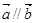 ,则
,则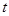 的值为
的值为  时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:不详 题型:解答题
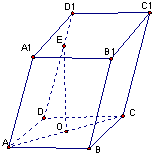
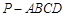 的底面
的底面 是直角梯形,
是直角梯形,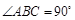 ,
,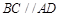 ,且
,且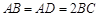 ,顶点
,顶点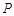 在底面
在底面 内的射影恰好落在
内的射影恰好落在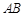 的中点
的中点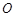 上.
上.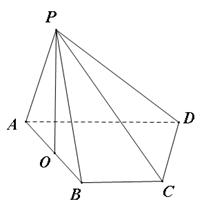
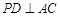 ;
;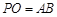 ,求直线
,求直线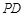 与
与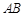 所成角的 余弦值;
所成角的 余弦值;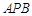 与平面
与平面 所成的二面角为
所成的二面角为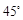 ,求
,求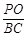 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
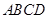 为直角梯形,
为直角梯形,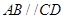 ,
,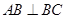 ,
,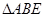 为等边三角形,且平面
为等边三角形,且平面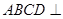 平面
平面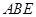 ,
,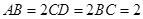 ,
,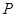 为
为 中点.
中点.
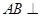
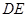 ;
;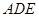 与平面
与平面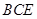 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;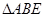 内是否存在一点
内是否存在一点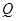 ,使
,使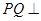 平面
平面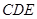 ,如果存在,求
,如果存在,求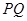 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| A1O |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AD |
| DE |
| 2 |
| 3 |
| DD1 |
| EO |
| AB |
| AD |
| AA1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
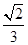 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
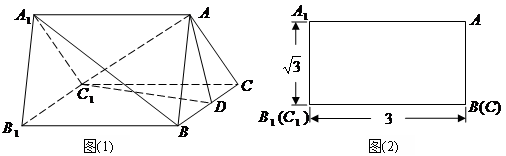
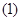 是一个水平放置的正三棱柱
是一个水平放置的正三棱柱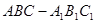 ,
,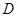 是棱
是棱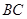 的中点.正三棱柱的主视图如图
的中点.正三棱柱的主视图如图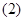 .
.
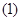 中垂直于平面
中垂直于平面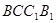 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)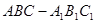 的体积;
的体积;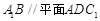 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com