
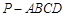 的底面
的底面 是直角梯形,
是直角梯形,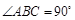 ,
,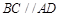 ,且
,且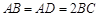 ,顶点
,顶点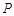 在底面
在底面 内的射影恰好落在
内的射影恰好落在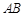 的中点
的中点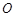 上.
上.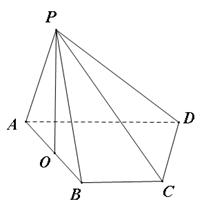
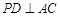 ;
;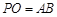 ,求直线
,求直线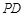 与
与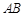 所成角的 余弦值;
所成角的 余弦值;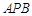 与平面
与平面 所成的二面角为
所成的二面角为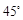 ,求
,求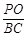 的值.
的值.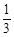 ;(3)
;(3) .
.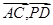 ,的坐标,代入数量积公式,验证其数量积与0的关系,即可得到结论.
,的坐标,代入数量积公式,验证其数量积与0的关系,即可得到结论. ,的坐标,代入向量夹角公式,即可求出直线PD与AB所成的角;
,的坐标,代入向量夹角公式,即可求出直线PD与AB所成的角;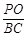 的值.
的值.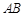 中点
中点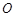 为点
为点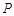 在平面
在平面 内的射影,所以
内的射影,所以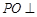 平面
平面 .过
.过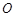 作
作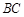 的平行线交
的平行线交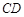 与点
与点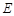 ,则
,则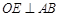 .
.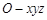 2分
2分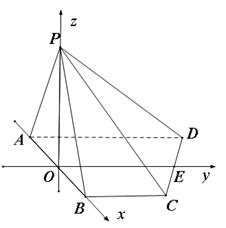
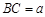 ,
,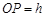 ,则
,则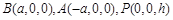 ,
,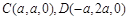 .
.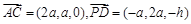 .
.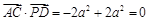 , ∴
, ∴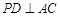 . 6分
. 6分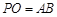 ,得
,得 ,于是
,于是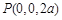
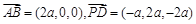 , 8分
, 8分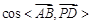
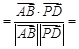
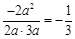 ,
,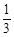 . 10分
. 10分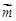 ,可得
,可得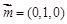 ,
, ,
,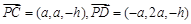 ,
,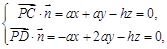 ∴
∴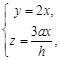 令
令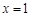 ,得到
,得到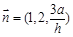 , 12分
, 12分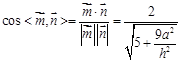 , 14分
, 14分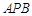 与平面
与平面 所成的二面角为
所成的二面角为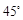 ,∴
,∴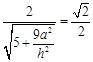 ,解得
,解得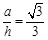 ,
, . 16分
. 16分

科目:高中数学 来源:不详 题型:解答题
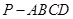 中,底面
中,底面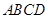 是边长为1的菱形,
是边长为1的菱形,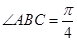 ,
,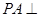 底面
底面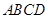 ,
,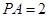 ,
,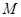 为
为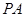 的中点,
的中点,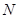 为
为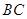 的中点,
的中点,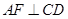 于
于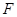 ,如图建立空间直角坐标系.
,如图建立空间直角坐标系.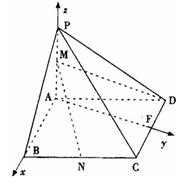
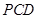 的一个法向量并证明
的一个法向量并证明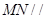 平面
平面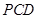 ;
;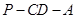 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).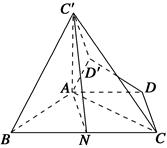
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| n |
| a |
A.若l⊥α,则
| B.若l∥α,则
| ||||||||
C.若
| D.若
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
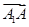 +
+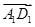 +
+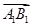 )2=3
)2=3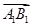 2;②
2;②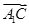 ·(
·(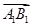 -
-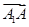 )=0;③向量
)=0;③向量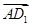 与向量
与向量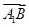 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|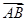 ·
·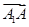 ·
·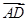 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
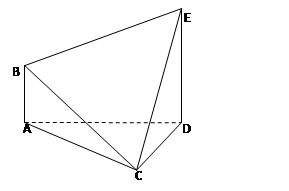
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com