Question

已知等比数列{a_n}的前n项和为S_n，a₁=2，S₁，2S₂，3S₃成等差数列．
（1）求数列{a_n}的通项公式；
（2）数列{b_n-a_n}是首项为-6，公差为2的等差数列，求数列{b_n}的前n项和．

Answer 1

解：（1）设等比数列{a_n}的公比为q，
∵S₁，2S₂，3S₃成等差数列，
∴4S₂=S₁+3S₃，
∵a₁=2，
∴4（2+2q）=2+6（1+q+q²），即3q²-q=0，解得q=0（舍去）或q=．
∴；
（2）由题意得b_n-a_n=2n-8，所以b_n=+2n-8．
设数列{b_n}的前n项和为T_n，则T_n=+=．
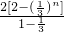
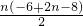
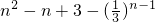
分析：（1）利用S₁，2S₂，3S₃成等差数列，确定数列的公比，即可求得数列的通项；
（2）确定数列{b_n}的通项，利用分组求和，可求数列{b_n}的前n项和．
点评：本题考查等差数列与等比数列的综合，考查数列的通项与求和，属于中档题．