
分析 (Ⅰ)不等式f(x)>|x-1|可化为|2x+3|>|x-1|,两边平方整理可解不等式;
(Ⅱ)求出f(x)-2g(x)的最小值是5,再利用“1”的代换,即可求出$\frac{1}{{a}^{2}}$+$\frac{9}{{b}^{2}}$的最小值.
解答 解:(Ⅰ)不等式f(x)>|x-1|,可化为|2x+3|>|x-1|,
两边平方整理可得(3x+2)(x+4)>0,
∴x>-$\frac{2}{3}$或x<-4,
∴不等式的解集为{x|x>-$\frac{2}{3}$或x<-4};
(Ⅱ)f(x)-2g(x)=|2x+3|+|2x-4|-2≥|2x+3-2x+4|-2=5,
∴f(x)-2g(x)的最小值是5,
∴m=5,
∴4a2+b2=5
∴$\frac{1}{{a}^{2}}$+$\frac{9}{{b}^{2}}$=$\frac{1}{5}$($\frac{1}{{a}^{2}}$+$\frac{9}{{b}^{2}}$)(4a2+b2)=$\frac{1}{5}$(13+$\frac{{b}^{2}}{{a}^{2}}$+$\frac{36{a}^{2}}{{b}^{2}}$)≥$\frac{1}{5}$(13+12)=5,
当且仅当$\frac{{b}^{2}}{{a}^{2}}$=$\frac{36{a}^{2}}{{b}^{2}}$且4a2+b2=5,即a2=$\frac{1}{2}$,b2=3时取等号,
∴$\frac{1}{{a}^{2}}$+$\frac{9}{{b}^{2}}$的最小值为5.
点评 本题考查绝对值不等式的解法,考查绝对值三角不等式的运用,考查基本不等式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,8) | B. | (8,+∞) | C. | (0,$\frac{1}{8}$) | D. | ($\frac{1}{8}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
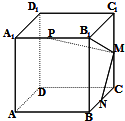 如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱CC1,BC,A1B1上的点,若∠B1MN=90°.则∠PMN的大小是( )
如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱CC1,BC,A1B1上的点,若∠B1MN=90°.则∠PMN的大小是( )| A. | 等于90° | B. | 小于90° | C. | 大于90° | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com