
【题目】在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M,N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( ) 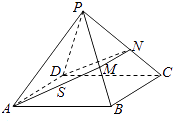
A.
B.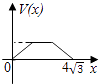
C.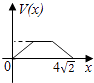
D.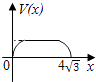
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布![]() ,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:

(注:表中试卷编号![]() )
)
(1)列出表中试卷得分为126分的试卷编号(写出具体数据);
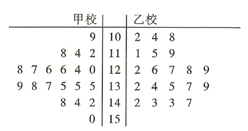
(2)该市又从乙校中也用系统抽样的方法抽取了20份试卷,将甲乙两校这40份试卷的得分制作了茎叶图(如图6),试通过茎叶图比较两校学生成绩的平均分及分散程度(均不要求计算出具体值,给出结论即可);
(3)在第(2)问的前提下,从甲乙两校这40名学生中,从成绩在140分以上(含140分)的学生中任意抽取3人,该3人在全市前15名的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
(附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a1+a3=10,S4=24.
(1)求数列{an}的通项公式;
(2)令Tn= ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为∠A、∠B、∠C所对的边,且 ![]() a=2csinA.
a=2csinA.
(1)确定∠C的大小;
(2)若c= ![]() ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列向量组中,能作为表示它们所在平面内所有向量的一组基底的是( )
A.![]() =(0,0)
=(0,0) ![]() =(1,﹣2)
=(1,﹣2)
B.![]() =(﹣1,2)
=(﹣1,2) ![]() =(3,7)
=(3,7)
C.![]() =(3,5)
=(3,5) ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3)
=(2,﹣3) ![]() =(
=( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(ex , lnx+k),
=(ex , lnx+k), ![]() =(1,f(x)),
=(1,f(x)), ![]() ∥
∥ ![]() (k为常数,e是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,F(x)=xexf′(x).
(k为常数,e是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,F(x)=xexf′(x).
(1)求k的值及F(x)的单调区间;
(2)已知函数g(x)=﹣x2+2ax(a为正实数),若对任意x2∈[0,1],总存在x1∈(0,+∞),使得g(x2)<F(x1),求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com