
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,使得
,使得![]() (
(![]() ),求实数
),求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时, ![]() 有极小值,极小值为
有极小值,极小值为![]() ,无极大值;(Ⅱ)
,无极大值;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的极值即可;
(Ⅱ)得到![]() , 设
, 设![]() 在
在![]() 上的值域为A,函数
上的值域为A,函数![]() 在
在![]() 上的值域为B,根据函数的单调性求出m的范围即可
上的值域为B,根据函数的单调性求出m的范围即可
试题解析:
(Ⅰ)依题意, ![]() ,
,
![]() ,
,
因为![]() ,故当
,故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
故当![]() 时,
时, ![]() 有极小值,极小值为
有极小值,极小值为![]() ,无极大值.
,无极大值.
(Ⅱ)当![]() =1时,
=1时, ![]()
因为![]() ,
, ![]() ,使得
,使得![]() ,
,
故![]() ;设
;设![]() 在
在![]() 上的值域为A,
上的值域为A,
函数![]() 在
在![]() 上的值域为B,
上的值域为B,
当![]() 时,
时, ![]() ,即函数
,即函数![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,又
,又![]() .
.
(i)当![]() 时,
时, ![]() 在
在![]() 上单调递减,此时
上单调递减,此时![]() 的值域为
的值域为![]() ,
,
因为![]() ,又
,又![]() ,故
,故![]() ,即
,即![]() ;
;
(ii)当![]() 时,
时, ![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() 的值域为
的值域为![]() ,因为
,因为![]() ,又
,又![]() ,
,
故![]() ,故
,故![]() ;
;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2≥a;命题q:x∈R,x2+2ax+2﹣a=0,若命题p∧q是真命题,则实数a的取值范围是( )
A.a≤﹣2或a=1
B.a≤﹣2或1≤a≤2
C.a≥1
D.﹣2≤a≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a1=3,其前n项和为Sn , 等比数列{bn}的各项均为正数,b1=1,公比为q(q≠0),且b2+S2=12, ![]() .
.
(1)求{an}与{bn}的通项公式;
(2)证明: ![]()
![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
污染 |
污染 |
污染 |
|
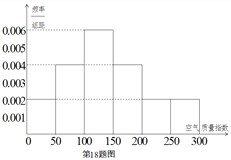
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
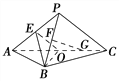
(Ⅰ)设G是OC的中点,证明:FG∥平面BOE;
(Ⅱ)证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M,N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( ) 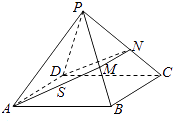
A.
B.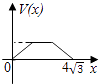
C.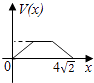
D.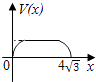
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣2x),g(x)=2cos2x,则下列结论正确的是( )
A.函数f(x)在区间[ ![]() ]上为增函数
]上为增函数
B.函数y=f(x)+g(x)的最小正周期为2π
C.函数y=f(x)+g(x)的图象关于直线x= ![]() 对称
对称
D.将函数f(x)的图象向右平移 ![]() 个单位,再向上平移1个单位,得到函数g(x)的图象
个单位,再向上平移1个单位,得到函数g(x)的图象
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com