
【题目】下列向量组中,能作为表示它们所在平面内所有向量的一组基底的是( )
A.![]() =(0,0)
=(0,0) ![]() =(1,﹣2)
=(1,﹣2)
B.![]() =(﹣1,2)
=(﹣1,2) ![]() =(3,7)
=(3,7)
C.![]() =(3,5)
=(3,5) ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3)
=(2,﹣3) ![]() =(
=( ![]() ,﹣
,﹣ ![]() )
)
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
污染 |
污染 |
污染 |
|
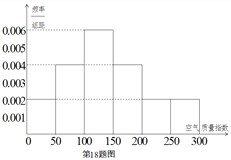
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M,N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( ) 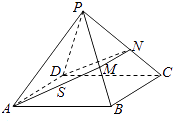
A.
B.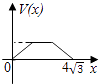
C.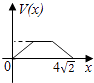
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设不等式组 ![]() 所表示的平面区域是W,从区域W中随机取点M(x,y).
所表示的平面区域是W,从区域W中随机取点M(x,y).
(1)若x,y∈Z,求点M位于第一象限的概率;
(2)若x,y∈R,求|OM|≥1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(2,0),B(0,1)两点.
=1(a>b>0)过点A(2,0),B(0,1)两点.
(1)求椭圆C的方程及离心率;
(2)设直线l与椭圆相交于不同的两点A,B.已知点A的坐标为(﹣a,0),点 Q(0,y0)在线段AB的垂直平分线上,且 ![]()
![]() =4,求y0的值.
=4,求y0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣2x),g(x)=2cos2x,则下列结论正确的是( )
A.函数f(x)在区间[ ![]() ]上为增函数
]上为增函数
B.函数y=f(x)+g(x)的最小正周期为2π
C.函数y=f(x)+g(x)的图象关于直线x= ![]() 对称
对称
D.将函数f(x)的图象向右平移 ![]() 个单位,再向上平移1个单位,得到函数g(x)的图象
个单位,再向上平移1个单位,得到函数g(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=4an﹣3(n∈N*).
(Ⅰ)证明:数列{an}是等比数列;
(Ⅱ)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com