
分析 (Ⅰ)当a=1时,不等式即|x-1|+|x+1|-x-2>0,等价于$\left\{\begin{array}{l}x≤1\\ 1-x+({-x-1})-x-2>0\end{array}\right.$或$\left\{\begin{array}{l}-1<x<1\\({1-x})+x+1-x-2>0\end{array}\right.$或$\left\{\begin{array}{l}x≥1\\({x-1})+({x+1})-x-2>0\end{array}\right.$,即可求不等式f(x)>0的解集;
(Ⅱ)当x∈[-a,1)时,f(x)=a-x-1,不等式f(x)≤0可化为a≤x+1,若存在x0∈[-a,1),使得f(x0)≤0,即可求a的取值范围.
解答 解:(Ⅰ)当a=1时,不等式即|x-1|+|x+1|-x-2>0,
等价于$\left\{\begin{array}{l}x≤1\\ 1-x+({-x-1})-x-2>0\end{array}\right.$或$\left\{\begin{array}{l}-1<x<1\\({1-x})+x+1-x-2>0\end{array}\right.$或$\left\{\begin{array}{l}x≥1\\({x-1})+({x+1})-x-2>0\end{array}\right.$
解得x≤-1或-1<x<0或x>2,
即不等式f(x)>0的解集为(-∞,0)∪(2,+∞).
(Ⅱ)当x∈[-a,1)时,f(x)=a-x-1,不等式f(x)≤0可化为a≤x+1,
若存在x0∈[-a,1),使得f(x0)≤0,则a<2,
所以a的取值范围为(-1,2).
点评 本题考查不等式的解法,考查存在性问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
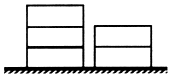 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )| A. | 6 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2017 | B. | 2016 | C. | 2 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com