
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 举出反例:f(x)=$\left\{\begin{array}{l}2x,x≤1\\-x+3,x>1\end{array}\right.$.g(x)=$\left\{\begin{array}{l}2x+3,x≤0\\-x+3,0<x<1\\ 2x,x≥1\end{array}\right.$,h(x)=$\left\{\begin{array}{l}-x,x≤0\\ 2x,x>0\end{array}\right.$,可判断①;
根据函数的周期性的定义,可判断②;根据函数奇偶性的性质,可判断③.
解答 解:①不成立.可举反例:f(x)=$\left\{\begin{array}{l}2x,x≤1\\-x+3,x>1\end{array}\right.$.g(x)=$\left\{\begin{array}{l}2x+3,x≤0\\-x+3,0<x<1\\ 2x,x≥1\end{array}\right.$,h(x)=$\left\{\begin{array}{l}-x,x≤0\\ 2x,x>0\end{array}\right.$.均不是增函数,
但f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均为增函数,
故①错误;
②∵f(x)+g(x)=f(x+T)+g(x+T),f(x)+h(x)=f(x+T)+h(x+T),
h(x)+g(x)=h(x+T)+g(x+T),
前两式作差可得:g(x)-h(x)=g(x+T)-h(x+T),
结合第三式可得:g(x)=g(x+T),h(x)=h(x+T),
同理可得:f(x)=f(x+T),因此②正确.
③若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是奇函数,
f(x)+g(x)+f(x)+h(x)-[g(x)、h(x)]=2f(x)是奇函数,
即f(x)是奇函数,
同理g(x)、h(x)均是奇函数,故③正确;
故选:C.
点评 本题考查了抽象函数的单调性,奇偶性与周期性、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | m | C. | 2m | D. | 4m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
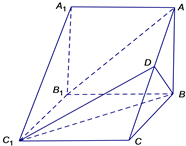 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
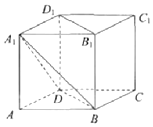 如图,在正方体ABCD-A1B1C1D1中,AB=2,平面α经过B1D1,直线AC1∥α,则平面α截该正方体所得截面的面积为( )
如图,在正方体ABCD-A1B1C1D1中,AB=2,平面α经过B1D1,直线AC1∥α,则平面α截该正方体所得截面的面积为( )| A. | 2$\sqrt{3}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{34}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在平面直角坐标系中有三条直线l1,l2,l3,其对应的斜率分别为k1,k2,k3,则下列选项中正确的是( )
如图,在平面直角坐标系中有三条直线l1,l2,l3,其对应的斜率分别为k1,k2,k3,则下列选项中正确的是( )| A. | k3>k1>k2 | B. | k1-k2>0 | C. | k1•k2<0 | D. | k3>k2>k1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com