
����Ŀ���˿������ǵ�����������ձ��ע������.��ʶ�˿������ı仯���ɣ�����Ϊ��Ч�����˿������ṩ����.����1798�꣬Ӣ������ѧ��������˹��T.R.Malthus��1766��1834�����������Ȼ״̬�µ��˿�����ģ�ͣ� ![]() ������x��ʾ������ʱ�䣬
������x��ʾ������ʱ�䣬 ![]() ��ʾx=0ʱ���˿ڣ�r��ʾ�˿ڵ�ƽ��������.
��ʾx=0ʱ���˿ڣ�r��ʾ�˿ڵ�ƽ��������.
�±���1950�D1959���ҹ��˿��������ϣ�

����Ը����˿������ʵ�ƽ��ֵ��Ϊ�ҹ���һʱ�ڵ��˿������ʣ���������˹�˿�����ģ�ͽ����ҹ���һʱ�ڵľ����˿�����ģ�ͣ�ijͬѧ����ͼ�μ���������������̽����
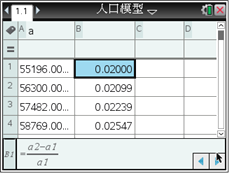
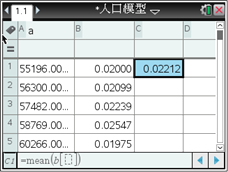
�ɴ˿ɵõ��ҹ�1950�D1959���ҹ���һʱ�ڵľ����˿�����ģ��Ϊ____________. ����ȷ��0.001��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() ��
��
��1��������y=f��x���ڵ㣨e��f��e��������������ֱ��x��2=0��ֱ����f��x���ĵ������䣨����eΪ��Ȼ�����ĵ�������
��2����������x1��x2��0��f��x1����f��x2����x1��x2���������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��a��0���� ����a=��3ʱ����f��x���ĵ����ݼ����䣻
��a��0���� ����a=��3ʱ����f��x���ĵ����ݼ����䣻
����������f��x�����ҽ���һ����㣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���ռ�����֪ʶ����ǿѧ���Ļ�����ʶ����ȫУ��֯��һ���йػ���֪ʶ�ľ����������������������ס������������ӣ�ÿ��3�ˣ������˾������涨ÿ�˻ش�һ�����⣬���Ϊ����Ӯ��10�֣������0�֣��������ÿ�˴�Եĸ��ʾ�Ϊ ![]() ���Ҷ���3�˴�Եĸ��ʷֱ�Ϊ
���Ҷ���3�˴�Եĸ��ʷֱ�Ϊ ![]() ��
�� ![]() ��
�� ![]() ���Ҹ��˻ش���ȷ����֮��û��Ӱ�죬�æα�ʾ�Ҷӵ��ܵ÷֣� ������εķֲ��к���ѧ������
���Ҹ��˻ش���ȷ����֮��û��Ӱ�죬�æα�ʾ�Ҷӵ��ܵ÷֣� ������εķֲ��к���ѧ������
������ס��������ܵ÷�֮�͵���30���Ҽӻ�ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������P��ABCD�У�PD�͵���ABCD������ABCDΪ�����Σ�PD��DC��F��PB���е㣮��֤��

(1)DF��AP.
(2)���߶�AD���Ƿ���ڵ�G��ʹGF��ƽ��PBC�������ڣ�˵��G���λ�ã���֤����Ľ��ۣ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��f(x)�ڶ�����[��1��1]�ϼ����溯�������Ǽ�������
(1)��֤��������x1��x2��[��1��1]����[f(x1)��f(x2)]��(x1��x2)��0��
(2)��f(1��a)��f(1��a2)��0����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ij����80���ˣ����о���һ������������з�ʽ�Ƿ����Ա��йأ��õ���������ݱ���
���з�ʽ | ������ | �˶� | �ϼ� |
���� | 20 | 10 | 30 |
�� | 45 | 5 | 50 |
�ϼ� | 65 | 15 | 80 |
��1������������Ƶ�ʹ���Ϊ����ĸ��ʣ��������3���ڸ����������ԣ�������3�������˶�Ϊ���з�ʽ������Ϊ�������X����X�ķֲ��к�������
��2�������������ݣ��ܷ���99%�İ�����Ϊ���з�ʽ���Ա��й�ϵ��
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ��K2= ![]() ��������n=a+b+c+d��
��������n=a+b+c+d��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� f��x��=asinx��bcosx��a��bΪ������a��0��x��R����x= ![]() ��ȡ����Сֵ������g��x��=f��
��ȡ����Сֵ������g��x��=f�� ![]() ��x���ǣ� ��
��x���ǣ� ��
A.ż����������ͼ����ڵ㣨�У�0���Գ�
B.�溯��������ͼ����ڵ㣨�У�0���Գ�
C.�溯��������ͼ����ڵ㣨 ![]() ��0���Գ�
��0���Գ�
D.ż����������ͼ����ڵ㣨 ![]() ��0���Գ�
��0���Գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R������f��x������f��2x��=x2��2ax+a2��1��
������f��x���Ľ���ʽ����д��f��x���Ķ�����
������f��x���� ![]() �ϵ�ֵ��Ϊ[��1��0]����ʵ��a��ȡֵ��Χ��
�ϵ�ֵ��Ϊ[��1��0]����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com